Page 134 - Modern Control Systems

108 Chapter 2 Mathematical Models of Systems

We select the coefficients where b/M = 3, k/M = 2, F{t)/M s = Q{t), and we
consider the initial conditions y(0) = - 1 and y(0) = 2. We then obtain the Laplace
transform equation, when the force, and thus Q(t), is a step function, as follows:
2
(s Y(s) - sy(0) - y(0)) + 3(sY(s) - y(0)) + 2Y{s) = ~Q(s). (2.132)
Since Q(s) = P/s, where P is the magnitude of the step function, we obtain

2
(s Y(s) + s - 2) + 3(sY(s) + 1) + 2Y(s) = - - ,

or 2
~(s + s + P)
(s 2 + 35 + 2)Y(s) = (2.133)
Thus the output transform is

-(s 2 + s + P) -(s 2 + s + P)
Y{s) = 2 (2.134)
s(s + 3s + 2) s(s + l)(s + 2)'
Expanding in partial fraction form yields

W + (2.135)
S 5 + 1 s + 2
We then have
-(5 2 + 5 + P) P_
* i (2.136)
(5 + 1)(5 + 2) s=0 2*
-P - 2
Similarly, k 2= +P and /c 3 =
. Thus,

3.0
:
2.8
j
j
2.6
2.4
/
2.2
2.0

1.8
1.6 '

1.4

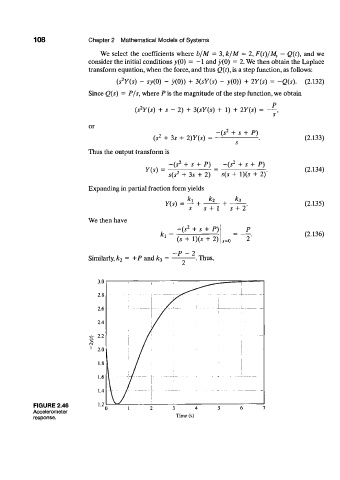
FIGURE 2.46 1.2 0 2 3 4 5 6 7
Accelerometer
response. Time (s)