Page 353 - Modern Control Systems

Section 5.6 The Steady-State Error of Feedback Control Systems 327

/?(s) *• tt.v)

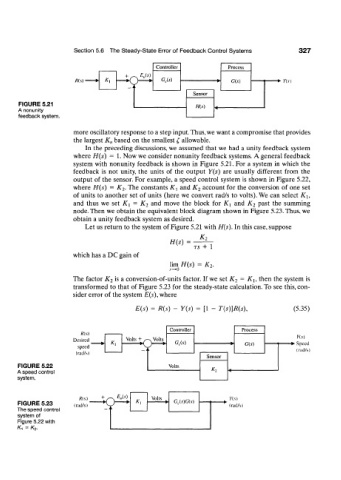
FIGURE 5.21
A nonunity
feedback system.

more oscillatory response to a step input. Thus, we want a compromise that provides
the largest K v based on the smallest t, allowable.
In the preceding discussions, we assumed that we had a unity feedback system
where H(s) = 1. Now we consider nonunity feedback systems. A general feedback
system with nonunity feedback is shown in Figure 5.21. For a system in which the
feedback is not unity, the units of the output Y(s) are usually different from the
output of the sensor. For example, a speed control system is shown in Figure 5.22,
where H(s) = K 2. The constants K\ and K 2 account for the conversion of one set
of units to another set of units (here we convert rad/s to volts). We can select K\,
and thus we set K\ = K 2 and move the block for K\ and K 2 past the summing
node. Then we obtain the equivalent block diagram shown in Figure 5.23. Thus, we
obtain a unity feedback system as desired.
Let us return to the system of Figure 5.21 with H(s). In this case, suppose

TS + 1
which has a DC gain of
limtfOv) K 7.
v—»0
The factor K 2 is a conversion-of-units factor. If we set K 2 = K h then the system is
transformed to that of Figure 5.23 for the steady-state calculation. To see this, con-
sider error of the system E(s), where
E(s) = R(s) - Y(s) = [1 - T(s)]R(s), (5.35)

Controller Process
Y(s)
Desired Volts + / - . Volts
G,(.v) - • Speed
speed — K J — • G(s)
(rad/s) (rad/s)
Sensor
FIGURE 5.22 Volts
A speed control K,
system.

R(s) Volts K(.v)
FIGURE 5.23 (rad/s) QZL G,(.v)G(.v) (rad/s)
The speed control
system of
Figure 5.22 with
/C| = K 2.