Page 135 - Modern physical chemistry

126 Relationships between Phases

then holds. Similarly for constituent B, we have

P B =x BP3, [6.51]
where X B is the mole fraction of B in the condensed phase while P B is the partial pres-
sure of B in the gas phase and p B is the vapor pressure of pure B at the given tempera-
Q
ture. When equations (6.50) and (6.51) hold at all concentrations, the solution is said to
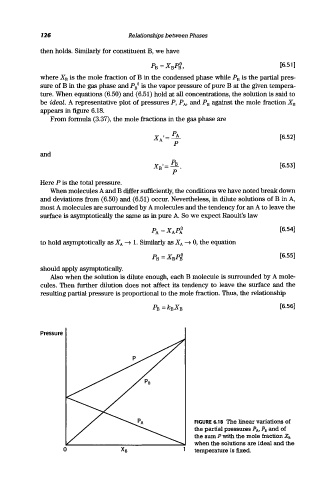
be ideal. A representative plot of pressures P, PA' and P B against the mole fraction X B
appears in figure 6.18.
From formula (3.37), the mole fractions in the gas phase are
,_PA
X A-- [6.52]
P
and

X B '= P B • [6.53]
P
Here P is the total pressure.
When molecules A and B differ sufficiently, the conditions we have noted break down
and deviations from (6.50) and (6.51) occur. Nevertheless, in dilute solutions of B in A,
most A molecules are surrounded by A molecules and the tendency for an A to leave the
surface is asymptotically the same as in pure A So we expect Raoult's law

PA =xAP1 [6.54]
to hold asymptotically as X A --t 1. Similarly as X A --t 0, the equation

PB =xBP3 [6.55]
should apply asymptotically.
Also when the solution is dilute enough, each B molecule is surrounded by A mole-
cules. Then further dilution does not affect its tendency to leave the surface and the
resulting partial pressure is proportional to the mole fraction. Thus, the relationship

[6.56]

Pressure

FIGURE 6.18 The linear variations of
the partial pressures PAl P B and of
the sum P with the mole fraction X B
when the solutions are ideal and the
temperature is fixed.