Page 139 - Modern physical chemistry

130 Relationships between Phases

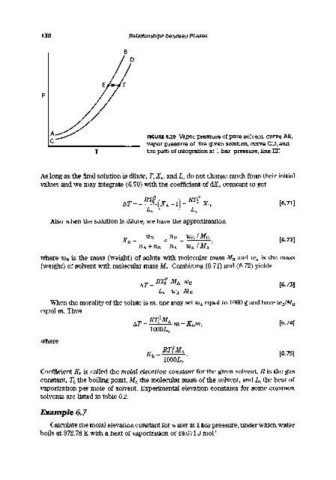
B

p

A FIGURE 6.20 Vapor pressure of pure solvent, curve AB,
C vapor pressure of the given solution, curve CD, and
T the path of integration at I bar pressure, line EF.

As long as the final solution is dilute, T, XA> and Lv do not change much from their initial
values and we may integrate (6.70) with the coefficient of dX A constant to get

I!.T = - RTo2 (X A -1) = RTo2 X B' [6.71 ]
Lv Lv
Also when the solution is dilute, we have the approximation

X = nB ~ _n_B = WB 1MB , [6.72]
B
nA +nB nA WA I MA
where Ws is the mass (weight) of solute with molecular mass Ms and W A is the mass
(weight) of solvent with molecular mass M A • Combining (6.71) and (6.72) yields

I!.T = RTo2 MA WB . [6.73]
Lv WA MB
When the morality of the solute is m, one may set W A equal to 1000 g and have wslMs
equal m. Thus
I!.T = RTo2 M A m = K m [6.74]
1000L b ,
v
where
K _ RTo2MA [6.75]
b - 1000L v

Coefficient Kb is called the molal elevation constant for the given solvent, R is the gas
constant, To the boiling point, MA the molecular mass of the solvent, and Lv the heat of
vaporization per mole of solvent. Experimental elevation constants for some common
solvents are listed in table 6.2.
Example 6.7

Calculate the molal elevation constant for water at 1 bar pressure, under which water
boils at 372.78 K with a heat of vaporization of 40,671 J mot l •