Page 141 - Modern physical chemistry

132 Relationships between Phases

B

p

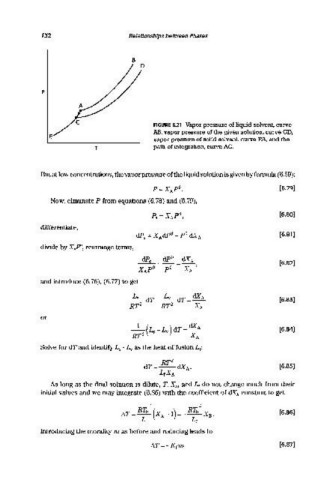
FIGURE 6.21 Vapor pressure of liquid solvent, curve
AB, vapor pressure of the given solution, curve CD,
vapor pressure of solid solvent, curve EA, and the
T path of integration, curve AC.

But at low concentrations, the vapor pressure of the liquid solution is given by formula (6.59):

P=XAPO. [6.79]
Now, eliminate P from equations (6.78) and (6.79),

[6.80]
differentiate,
dP s =XAdPO +p o dXp, [6.81]

divide by XAPl, rearrange terms,
dP s dPo dX A [6.82]
XApO - pO = X A '
and introduce (6.76), (6.77) to get

[6.83]

or
_l_(Ls - Lv) dT = dX A • [6.84]
RT2 X A

Solve for dT and identify Ls - Lv as the heat of fusion L f :

dT= RT2 dX . [6.85]
LrX A A
As long as the final solution is dilute, T, X A , and L f do not change much from their
initial values and we may integrate (6.85) with the coefficient of dX A constant to get

2 2
[6.86]
ilT= R~ (XA -1)=- R~ X B •
IntrodUCing the morality m as before and reducing leads to

[6.87]