Page 82 - Book Hosokawa Nanoparticle Technology Handbook

FUNDAMENTALS CH. 2 STRUCTURAL CONTROL OF NANOPARTICLES
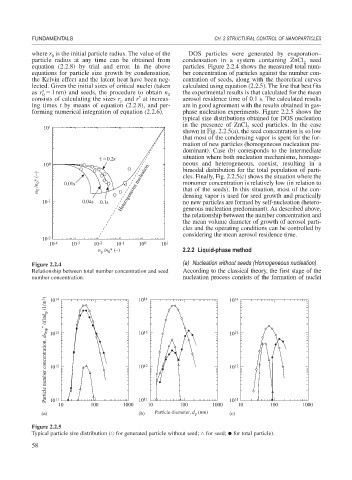
where r is the initial particle radius. The value of the DOS particles were generated by evaporation–
0
particle radius at any time can be obtained from condensation in a system containing ZnCl seed
2
equation (2.2.8) by trial and error. In the above particles. Figure 2.2.4 shows the measured total num-
equations for particle size growth by condensation, ber concentration of particles against the number con-
the Kelvin effect and the latent heat have been neg- centration of seeds, along with the theoretical curves
lected. Given the initial sizes of critical nuclei (taken calculated using equation (2.2.5). The line that best fits
*
as r 1nm) and seeds, the procedure to obtain n T the experimental results is that calculated for the mean
0
*
consists of calculating the sizes r and r at increas- aerosol residence time of 0.1 s. The calculated results
p
ing times t by means of equation (2.2.8), and per- are in good agreement with the results obtained in gas-
forming numerical integration of equation (2.2.6). phase nucleation experiments. Figure 2.2.5 shows the
typical size distributions obtained for DOS nucleation
in the presence of ZnCl seed particles. In the case
10 1 2
shown in Fig. 2.2.5(a), the seed concentration is so low
that most of the condensing vapor is spent for the for-
mation of new particles (homogeneous nucleation pre-
dominant). Case (b) corresponds to the intermediate
situation where both nucleation mechanisms, homoge-
τ = 0.2s
10 0 neous and heterogeneous, coexist, resulting in a
bimodal distribution for the total population of parti-
n T /n 0 * (−) 0.01s Heterogeneous nucleation cles. Finally, Fig. 2.2.5(c) shows the situation where the
monomer concentration is relatively low (in relation to
that of the seeds). In this situation, most of the con-
no new particles are formed by self-nucleation (hetero-
10 -1 0.04s 0.1s densing vapor is used for seed growth and practically
geneous nucleation predominant). As described above,
the relationship between the number concentration and
the mean volume diameter of growth of aerosol parti-
cles and the operating conditions can be controlled by
considering the mean aerosol residence time.
10 -2
10 -4 10 -3 10 -2 10 -1 10 0 10 1
n /n * (−) 2.2.2 Liquid-phase method
p
0
Figure 2.2.4 (a) Nucleation without seeds (Homogeneous nucleation)
Relationship between total number concentration and seed According to the classical theory, the first stage of the
number concentration. 10 14 nucleation process consists of the formation of nuclei

Particle number concentration, dn exp * /dlnd p (1/m 3 ) 10 13 10 13 10 13
10 14
10 14

12
12
10
12
10
10
11
10
10 100 1000 10 11 10 100 1000 10 11 10 100 1000
(a) (b) Particle diameter, d (nm) (c)
p
Figure 2.2.5
Typical particle size distribution ( for generated particle without seed; for seed; for total particle).
58