Page 84 - Book Hosokawa Nanoparticle Technology Handbook

FUNDAMENTALS CH. 2 STRUCTURAL CONTROL OF NANOPARTICLES
Table 2.2.1 shows an example of controlling the par- (b) Nucleation with seeds (Heterogeneous nucleation)
ticle size of silver particles generated by chemical When particles are present in the system, we must
reduction. It can be seen that the size of the generated consider two types of condensation processes:
particle decreases with increasing solution viscosity. condensation of monomers onto the seed surfaces
The diffusion coefficient of monomers is inversely (heterogeneous nucleation) and self-nucleation of
proportional to the solution viscosity. The nucleation monomers (homogeneous nucleation). The model
time was constant regardless of the solution viscosity. for both homogeneous and heterogeneous nucle-
The other parameters included in equation (2.2.13) can ation is based on the development presented in the
be considered to be constant. Therefore, since the num- former section for homogeneous nucleation, using a
ber concentration of generated particles increases in cell model. To reproduce the experimental results of
proportion to the solution viscosity, the final size of the nucleation in the presence of seeds, modification of
generated particles decreases with equation (2.2.14). In the cell model is necessary. The constant size cell
addition, the mean diameter of the generated particles model assumes that all the particles are equally
can be estimated using these relational expressions. spaced. Actually, the particles are distributed ran-
domly in the medium, so that the distances between
neighboring particles follow a certain distribution
10 17
law. Monomers generated in regions where the seeds
are separated by very small distances are soon
depleted through condensation onto the seed surfaces.
particle number concentration (1/m 3 ) 10 15 fraction of the total number of cells. Hence, the
Conversely, new nuclei can only be formed in those
10 16
places where the distance between particles is larger.
We assume now that new nuclei can be formed with a
*
number concentration of self-nucleated particles is
* *
given by n , because the number concentration of
0
homogeneously nucleated particles without seeds is
*
n . When the system contains seeds of radius r and
p
0
number concentration n , the total particle number
p
concentration after nucleation in a system containing
10 14
seed particles n is given by [2]
T
⎧ ⎪ n 1( R n ) ( n n )
*
n ⎨ 0 p p pc (2.2.16)
T
**
10 13 ⎩ ⎪ nv n p ( n n )
0
p
pc
10 13 10 14 10 15 10 16 10 17
1 * * *
(1/m 3 ) where R r /r , n n (1– )/R.
4πr*Dt* p pc 0
Silver particles were generated by chemical reduc-
tion in a system containing silver seed particles.
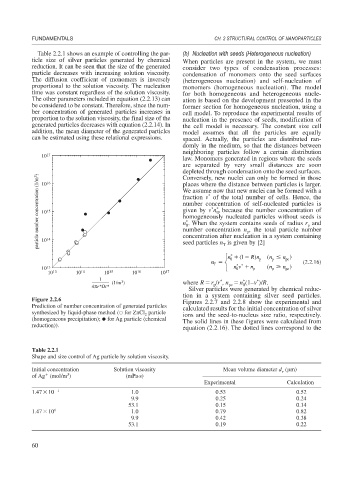
Figure 2.2.6 Figures 2.2.7 and 2.2.8 show the experimental and
Prediction of number concentration of generated particles calculated results for the initial concentration of silver
synthesized by liquid-phase method ( for ZnCl particle ions and the seed-to-nucleus size ratio, respectively.
2
(homogeneous precipitation); for Ag particle (chemical The solid lines in these figures were calculated from
reduction)).
equation (2.2.16). The dotted lines correspond to the
Table 2.2.1
Shape and size control of Ag particle by solution viscosity.
Initial concentration Solution viscosity Mean volume diameter d ( m)
v

3
of Ag (mol/m ) (mPa·s)
Experimental Calculation
1.47
10 1 1.0 0.53 0.52
9.9 0.25 0.24
53.1 0.15 0.14
1.47
10 1 1.0 0.79 0.82
9.9 0.42 0.38
53.1 0.19 0.22
60