Page 296 - Numerical Analysis Using MATLAB and Excel

Chapter 7 Finite Differences and Interpolation

Interpolation with Newton's Divided Difference Formula
f(x) = f(x )+(x-x )f(x ,x )+(x-x )(x-x )f(x ,x ,x )+(x-x )(x-x )(x-x )f(x ,x ,x ,x )
1
1
0
0
0
0
0
1
1
0
3
2
0
2
2
1
In this example, w e w ant to evaluate f(x) at x= 2
1st divided 2nd divided 3rd divided
difference difference difference
x f(x) f(x , x ) f(x , x , x ) f(x ,x ,x ,x )
0 1 0 1 2 0 1 2 3
-1.00 3.000
-5.000
0.00 -2.000 5.500
3.250 -1.000
0.50 -0.375 3.500
6.750 -1.000
1.00 3.000 1.000
8.750 -1.000
2.50 16.125 -1.500
5.750
3.00 19.000
We use the above formula w ith starting value x0.00
f(2)=B12+(E3-E18)*C13+(E3-E18)*(E3-A14)*D14+(E3-E18)*(E3-A14)*(E3-A16)*E15
or f(2)= 12.00
The plot below verifies that our answ er is correct
-1.000 3.000
0.000 -2.000 20
15
0.500 -0.375 f(x) 10
1.000 3.000 5
0
2.500 16.125 -5
3.000 19.000 -1.0 0.0 1.0 2.0 3.0
x
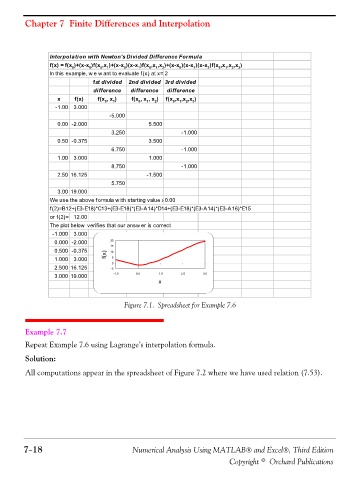
Figure 7.1. Spreadsheet for Example 7.6

Example 7.7
Repeat Example 7.6 using Lagrange’s interpolation formula.

Solution:
All computations appear in the spreadsheet of Figure 7.2 where we have used relation (7.53).

7−18 Numerical Analysis Using MATLAB® and Excel®, Third Edition
Copyright © Orchard Publications