Page 300 - Numerical Analysis Using MATLAB and Excel

Chapter 7 Finite Differences and Interpolation

Gregory-Newton Forward Interpolation Method

See expressions (7.54) and (7.55)

Interpolate f(x) at x= 1.03

x f(x) Δf Δ2f Δ3f
1.00 1.000000
0.257625
1.05 1.257625 0.015750
0.273375 0.000750
1.10 1.531000 0.016500
0.289875 0.000750
1.15 1.820875 0.017250
0.307125 0.000750
1.20 2.128000 0.018000
0.325125
1.25 2.453125

h= A10-A8= 0.05 r= (D5-A8)/C20=0.6

f(1.12)=B8+F20*C9+(F20*(F20-1)*D10)/FACT(2)+(F20*(F20-1)*(F20-2)*E11)/FACT(3)
= 1.152727

1.00 1.000000
1.05 1.257625 3.00
1.10 1.531000 2.50
1.15 1.820875 2.00
1.20 2.128000
1.25 2.453125 1.50
1.00
0.50
0.00
1.00 1.05 1.10 1.15 1.20 1.25

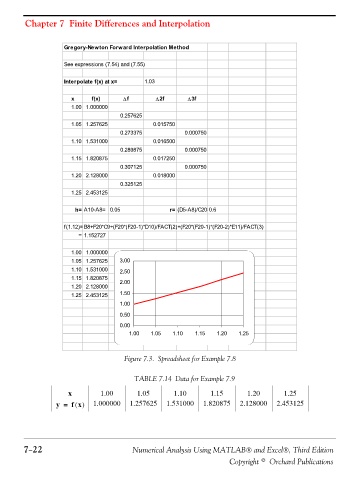
Figure 7.3. Spreadsheet for Example 7.8

TABLE 7.14 Data for Example 7.9

x 1.00 1.05 1.10 1.15 1.20 1.25
y = f x() 1.000000 1.257625 1.531000 1.820875 2.128000 2.453125

7−22 Numerical Analysis Using MATLAB® and Excel®, Third Edition
Copyright © Orchard Publications