Page 307 - Numerical Methods for Chemical Engineering

296 6 Boundary value problems

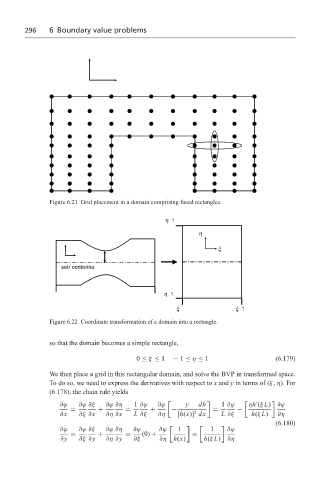
Figure 6.21 Grid placement in a domain comprising fused rectangles.

h 1
h

x

setr centerine

h 1
x x 1
Figure 6.22 Coordinate transformation of a domain into a rectangle.

so that the domain becomes a simple rectangle,

0 ≤ ξ ≤ 1 − 1 ≤ η ≤ 1 (6.179)

We then place a grid in this rectangular domain, and solve the BVP in transformed space.
To do so, we need to express the derivatives with respect to x and y in terms of (ξ, η). For
(6.178), the chain rule yields
∂ϕ ∂ϕ ∂ξ ∂ϕ ∂η 1 ∂ϕ ∂ϕ y dh 1 ∂ϕ ηh (ξ L) ∂ϕ

= + = + − = −
2
∂x ∂ξ ∂x ∂η ∂x L ∂ξ ∂η [h(x)] dx L ∂ξ h(ξ L) ∂η
(6.180)

∂ϕ ∂ϕ ∂ξ ∂ϕ ∂η ∂ϕ ∂ϕ 1 1 ∂ϕ
= + = (0) + =
∂y ∂ξ ∂y ∂η ∂y ∂ξ ∂η h(x) h(ξ L) ∂η