Page 339 - Numerical Methods for Chemical Engineering

328 7 Probability theory and stochastic simulation

12

1

disaceent 2

−2
−
−
−
1 1 2
ste ner
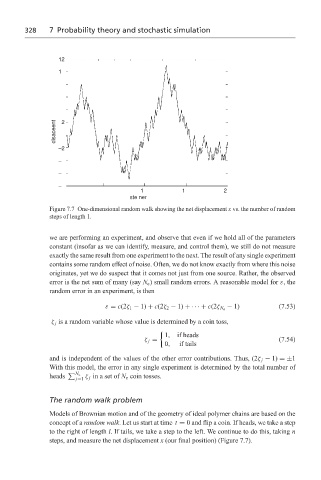
Figure 7.7 One-dimensional random walk showing the net displacement x vs. the number of random
steps of length 1.

we are performing an experiment, and observe that even if we hold all of the parameters
constant (insofar as we can identify, measure, and control them), we still do not measure
exactly the same result from one experiment to the next. The result of any single experiment
contains some random effect of noise. Often, we do not know exactly from where this noise
originates, yet we do suspect that it comes not just from one source. Rather, the observed
error is the net sum of many (say N e ) small random errors. A reasonable model for ε, the
random error in an experiment, is then

− 1) (7.53)
ε = c(2ζ 1 − 1) + c(2ζ 2 − 1) + ··· + c(2ζ N e
ζ j is a random variable whose value is determined by a coin toss,

1, if heads
ζ j = (7.54)
0, if tails
and is independent of the values of the other error contributions. Thus, (2ζ j − 1) =±1
With this model, the error in any single experiment is determined by the total number of
N e
heads j=1 ζ j in a set of N e coin tosses.

The random walk problem

Models of Brownian motion and of the geometry of ideal polymer chains are based on the
concept of a random walk. Let us start at time t = 0 and flip a coin. If heads, we take a step
to the right of length l. If tails, we take a step to the left. We continue to do this, taking n
steps, and measure the net displacement x (our final position) (Figure 7.7).