Page 128 - PRINCIPLES OF QUANTUM MECHANICS as Applied to Chemistry and Chemical Physics

4.3 Eigenfunctions 119

Energy V

ψ 3

7 hω n 5 3
2

ψ 2

5 hω n 5 2
2

ψ 1

3 hω n 5 1
2

ψ 0

1 hω n 5 0
2

x
0
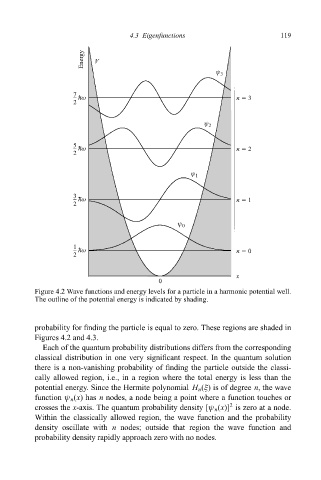
Figure 4.2 Wave functions and energy levels for a particle in a harmonic potential well.
The outline of the potential energy is indicated by shading.

probability for ®nding the particle is equal to zero. These regions are shaded in
Figures 4.2 and 4.3.
Each of the quantum probability distributions differs from the corresponding
classical distribution in one very signi®cant respect. In the quantum solution
there is a non-vanishing probability of ®nding the particle outside the classi-
cally allowed region, i.e., in a region where the total energy is less than the
potential energy. Since the Hermite polynomial H n (î)isofdegree n, the wave
function ø n (x) has n nodes, a node being a point where a function touches or
2
crosses the x-axis. The quantum probability density [ø n (x)] is zero at a node.
Within the classically allowed region, the wave function and the probability
density oscillate with n nodes; outside that region the wave function and
probability density rapidly approach zero with no nodes.