Page 130 - PRINCIPLES OF QUANTUM MECHANICS as Applied to Chemistry and Chemical Physics

4.4 Matrix elements 121
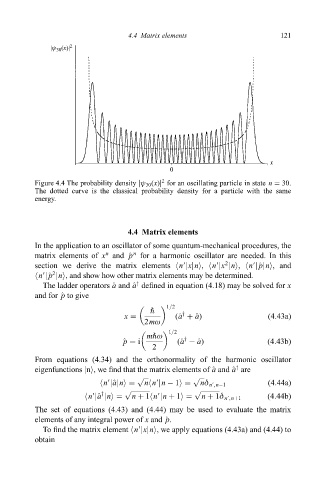
|ψ (x)| 2
30

x
0
2
Figure 4.4 The probability density jø 30 (x)j for an oscillating particle in state n ˆ 30.
The dotted curve is the classical probability density for a particle with the same
energy.

4.4 Matrix elements

In the application to an oscillator of some quantum-mechanical procedures, the
n
n
matrix elements of x and ^ p for a harmonic oscillator are needed. In this
2
section we derive the matrix elements hn9jxjni, hn9jx jni, hn9j^ pjni, and
2
hn9j^ p jni, and show how other matrix elements may be determined.
The ladder operators ^ a and ^ a de®ned in equation (4.18) may be solved for x
y
and for ^ p to give
1=2
"
y
x ˆ (^ a ‡ ^ a) (4:43a)
2mù
1=2
m"ù
^ p ˆ i (^ a ÿ ^ a) (4:43b)
y
2
From equations (4.34) and the orthonormality of the harmonic oscillator
y
eigenfunctions jni, we ®nd that the matrix elements of ^ a and ^ a are
p  p 
hn9j^ ajniˆ nhn9jn ÿ 1iˆ nä n9,nÿ1 (4:44a)
p  p 
y
hn9j^ a jniˆ n ‡ 1hn9jn ‡ 1iˆ n ‡ 1ä n9,n‡1 (4:44b)
The set of equations (4.43) and (4.44) may be used to evaluate the matrix
elements of any integral power of x and ^ p.
To ®nd the matrix element hn9jxjni, we apply equations (4.43a) and (4.44) to
obtain