Page 180 - Phase Space Optics Fundamentals and Applications

The Radon-Wigner Transform 161

1.00
Fractional correlation intensity 1.0
p
0.75

0.5
0.50

1.0
0.25 0.0 0.6 0.8
Fractional order p
0 0.2 0.4
0.00 Space coordinate (x) 0.0
0
x
(a)
1.00
p 1.0
Fractional correlation intensity 0.5
0.75

0.50

0.25 0.8
1.0
Fractional order p
0.00 0.0 0 0.2 0.4 0.6
0 Space coordinate (x) 0.0
x
(b)

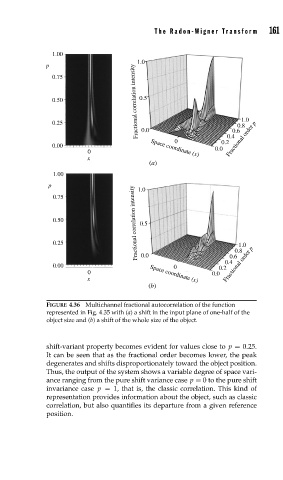
FIGURE 4.36 Multichannel fractional autocorrelation of the function
represented in Fig. 4.35 with (a) a shift in the input plane of one-half of the
object size and (b) a shift of the whole size of the object.

shift-variant property becomes evident for values close to p = 0.25.
It can be seen that as the fractional order becomes lower, the peak
degenerates and shifts disproportionately toward the object position.
Thus, the output of the system shows a variable degree of space vari-
ance ranging from the pure shift variance case p = 0 to the pure shift
invariance case p = 1, that is, the classic correlation. This kind of
representation provides information about the object, such as classic
correlation, but also quantifies its departure from a given reference
position.