Page 178 - Phase Space Optics Fundamentals and Applications

The Radon-Wigner Transform 159

Input plane Filter plane
x 0 a¢ x h
L c R p a p
l
z
BS
S
He-Ne
θ
t L
H
M 1 M 1

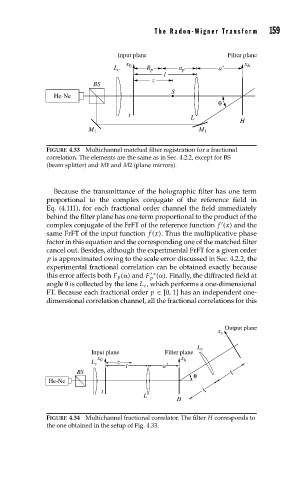
FIGURE 4.33 Multichannel matched filter registration for a fractional
correlation. The elements are the same as in Sec. 4.2.2, except for BS
(beam splitter) and M1 and M2 (plane mirrors).

Because the transmittance of the holographic filter has one term
proportional to the complex conjugate of the reference field in
Eq. (4.111), for each fractional order channel the field immediately
behind the filter plane has one term proportional to the product of the
complex conjugate of the FrFT of the reference function f (x) and the

same FrFT of the input function f (x). Thus the multiplicative phase
factor in this equation and the corresponding one of the matched filter
cancel out. Besides, although the experimental FrFT for a given order
p is approximated owing to the scale error discussed in Sec. 4.2.2, the
experimental fractional correlation can be obtained exactly because
this error affects both F p ( ) and F ( ). Finally, the diffracted field at
∗
p
angle is collected by the lens L c , which performs a one-dimensional
FT. Because each fractional order p ∈ [0, 1] has an independent one-
dimensional correlation channel, all the fractional correlations for this

Output plane
x c

L c
Input plane Filter plane
x 0 x h
L c z a¢
l
BS f
θ
He-Ne
t f
L
H
FIGURE 4.34 Multichannel fractional correlator. The filter H corresponds to
the one obtained in the setup of Fig. 4.33.