Page 214 - Pipeline Risk Management Manual Ideas, Techniques, and Resources

Data analyses 8/191

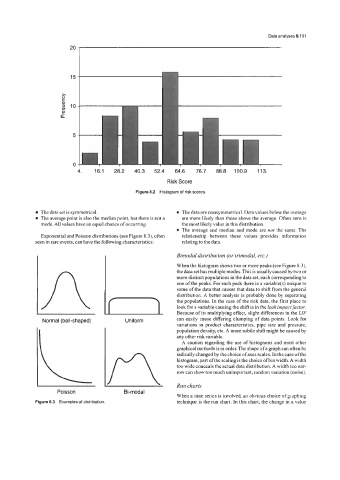
4. 16.1 28.2 40.3 52.4 64.6 76.7 88.8 100.9 113.
Risk Score
Figure 8.2 Histogram of riskscores.

The data set is symmetrical. The data are nonsymmetrical. Data values below the average
The average point is also the median point, but there is not a are more likely than those above the average. Often zero is
mode. All values have an equal chance of occurring. the most likely value in this distribution.
The average and median and mode are not the same. The
Exponential and Poisson distributions (see Figure 8.3), often relationship between these values provides information
seen in rare events, can have the following characteristics: relating to the data.
Bimodal distribution (or trimodal, etc.)
When the histogram shows two or more peaks (see Figure 8.3),
the data set has multiple modes. This is usually caused by two or
more distinct populations in the data set, each corresponding to
one of the peaks. For each peak there is a variable(s) unique to
n
some of the data that causes that data to shift from the general
distribution. A better analysis is probably done by separating
the populations. In the case of the risk data, the first place to
look for a variable causing the shift is in the leak impactfactor.
can easily cause differing clumping of data points. Look for
Normal (bell-shaped) Uniform Because of its multiplying effect, slight differences in the LZF
variations in product characteristics, pipe size and pressure,
population density, etc. A more subtle shift might be caused by
any other risk variable.
A caution regarding the use of histograms and most other
graphical methods is in order. The shape of a graph can often be
radically changed by the choice of axes scales. In the case of the
histogram, part ofthe scaling is the choice ofbin width. A width
too wide conceals the actual data distribution. A width too nar-
row can show too much unimportant, random variation (noise).

Run charts
Poisson Bi-modal
When a time series is involved, an obvious choice of graphing
Figure 8.3 Examples of distribution. technique is the run chart. In this chart, the change in a value