Page 172 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

A n U n d e r d a m p e d P ro c e s s 147

Time
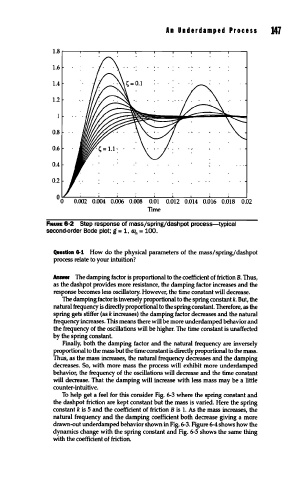
F1auRE 6-2 Step response of massjspringjdashpot process-typical
second-order Bode plot; g = 1, ron = 100.

Question 6-1 How do the physical parameters of the mass/spring/dashpot
process relate to your intuition?

Answer The damping factor is proportional to the coefficient of friction B. Thus,
as the dashpot provides more resistance, the damping factor increases and the
response becomes less oscillatory. However, the time constant will decrease.
The damping factor is inversely proportional to the spring constant k. But, the
natural frequency is directly proportional to the spring constant. Therefore, as the
spring gets stiffer (ask increases) the damping factor decreases and the natural
frequency increases. This means there will be more underdamped behavior and
the frequency of the oscillations will be higher. The time constant is unaffected
by the spring constant.
FinaUy, both the damping factor and the natural frequency are inversely
proportional to the mass but the time constant is directly proportional to the mass.
Thus, as the mass increases, the natural frequency decreases and the damping
decreases. So, with more mass the process will exhibit more underdamped
behavior, the frequency of the oscillations will decrease and the time constant
will decrease. That the damping will increase with less mass may be a little
counter-intuitive.
To help get a feel for this consider Fig. 6-3 where the spring constant and
the dashpot friction are kept constant but the mass is varied. Here the spring
constant k is 5 and the coefficient of friction B is 1. As the mass increases, the
natural frequency and the damping coefficient both decrease giving a more
drawn-out underdamped behavior shown in Fig. 6-3. Figure 6-4 shows how the
dynamics change with the spring constant and Fig. 6-5 shows the same thing
with the coefficient of friction.