Page 175 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

l50 Chapter Six

The poles of the transfer function are located at the roots of the
quadratic in the denominator:

If the damping factor {is less than unity, these poles become com-
plex conjugates and the solution will contain sinusoidal components
suggesting underdamped behavior, as in

where Euler's formula e"+ib = e"[cos(b) + jsin(b)] can be used to bring
in the sinusoids.
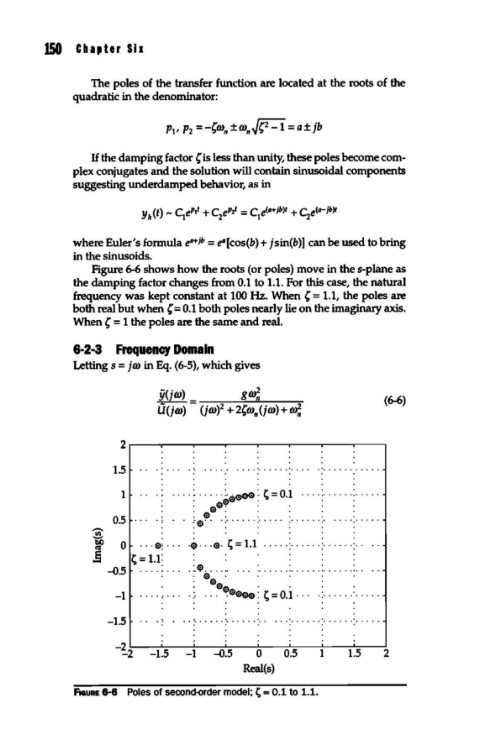
Figure 6-6 shows how the roots (or poles) move in the s-plane as
the damping factor changes from 0.1 to 1.1. For this case, the natural
frequency was kept constant at 100 Hz. When { = 1.1, the poles are
both real but when { = 0.1 both poles nearly lie on the imaginary axis.
When { = 1 the poles are the same and real.

6·2·3 Frequency Domain
Letting s = jro in Eq. (6-5), which gives

y(jro) _ gro; (6-6)
U(jro) - (jro) + 2{ro" (jro) + ro!
2

2.---~--~--~---,.---~--~--~---.
1.5 ..... .

1 . . . . ~ .... ·~eee<:> ~ ~ = 0.1 ... ·:· .... ·:· ....
. 0e. . . . .
: 0 . . . . .
0.5 :·e·· ............. . ........ .
' 0 ···EI:··· ·•···EI· ~=1.1 ..... : ...... : ...... : .. ··
t.= ~ = 1.t: . .
-0.5 .... : .... ~$ ......... : ...... : ...... : ...... : ..
00 .
. 0e . . . .
-1 ........ ·:· ... ~.00ee: ~=0.1 ... ·: ...... : .....
.
.
.
.
.
.
-1.5 0 0. 0 0 •••••••••••••••• 0. 0 ••••••••••••
I
I
I
I
0
I
-~2 -1.5 -1 -0.5 0 0.5 1 1.5 2
Real(s)
F1auRE 8-8 Poles of seconc::k»rder model; ~ = 0.1 to 1.1.