Page 179 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

154 Chapter Six

The real negative zero at s =-I/k from Gc will not cancel either of
2
the complex conjugate poles at -~ ± ~~ - 1 from GP. This suggests
that proportional plus integral control may not have much impact
on the complex poles that produce the underdamped behavior. The
presence of these complex conjugate poles poses a different control
challenge relative to that posed by the single water tank and the
three-tank process.
A more detailed approach will be given to tuning PI control algo-
rithms in Chap. 11 but for control of the dashpot process with ~ = 0.1 a
crude trial and error approach will suffice here. First, the proportional
gain k was chosen to be unity because the process has unity gain and a
good rule of thumb suggests that the process gain and the control gain
be reciprocals. The integral gain was another matter. We started with
conservative values of I and increased them until a semblance of accept-
able behavior was arrived at with I= 0.3.
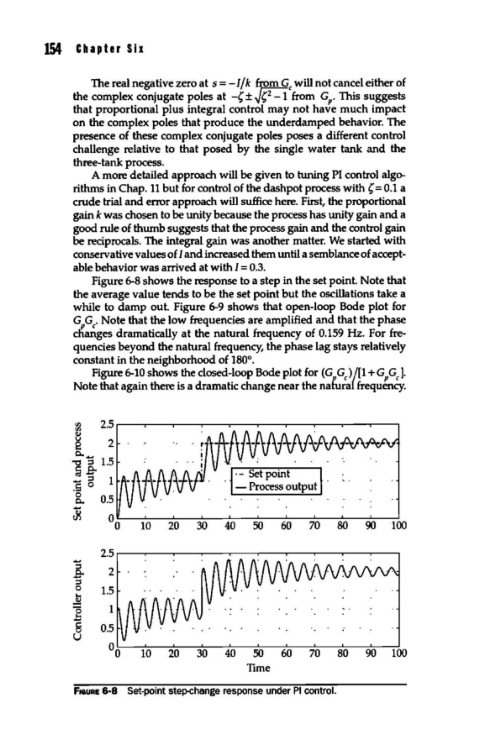
Figure 6-8 shows the response to a step in the set point. Note that
the average value tends to be the set point but the oscillations take a
while to damp out. Figure 6-9 shows that open-loop Bode plot for
GpGc. Note that the low frequencies are amplified and that the phase
changes dramatically at the natural frequency of 0.159 Hz. For fre-
quencies beyond the natural frequency, the phase lag stays relatively
constant in the neighborhood of 180°.
Figure 6-10 shows the closed-loop Bode plot for (G G)/[1 +G GJ
Note that again there is a dramatic change near the nahuai frequ:Ocy.

10 20 30 40 50 60 70 80 90 100

2.5
j 2
::s
0 1.5
.$!
0 1
l::
6 0.5
u

Trme
F1cauRE 6-8 Set-point step-change response under PI control.