Page 182 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

An Underda01ped Process l51

Chaps. 9 and 11. Furthermore, an overall control gain Kc has been intro-
duced to be consistent with wide usage among control engineers.
Unlike the PI control algorithm, PID has two zeros in the numera-
tor of Gc

2
U(s) = G = K s +I+ Ds
e(s) c c s
-1±~
sl' s2 = 2D

which can be complex conjugates if 4DI > 1. Therefore, these poten-
tially complex zeroes in G c might ameliorate the presence of the com-
plex poles in G,:

G G = 1 K s+l +Ds 2
P c s 2 +2{s+1 c s

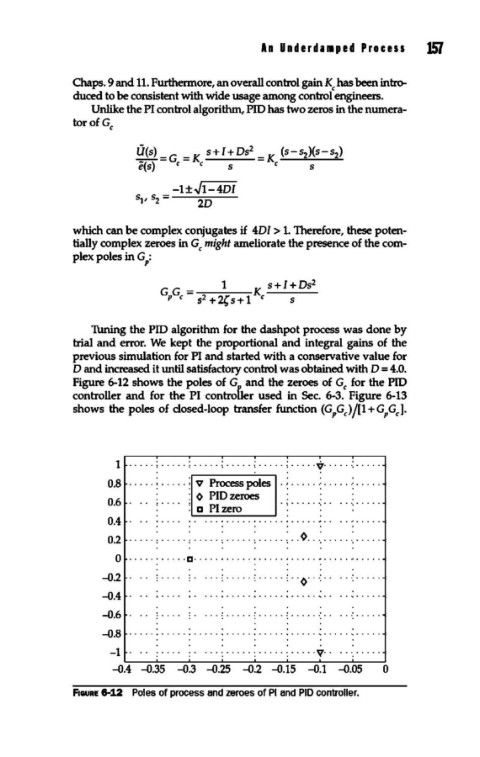
Thning the PID algorithm for the dashpot process was done by
trial and error. We kept the proportional and integral gains of the
previous simulation for PI and started with a conservative value for
D and increased it until satisfactory control was obtained with D = 4.0.
Figure 6-12 shows the poles of G and the zeroes of Gc for the PID
controller and for the PI controller used in Sec. 6-3. Figure 6-13
shows the poles of closed-loop transfer function (G,GJ/[1+G,Gc1·

1 ..... ; ..... ; ..... ; ..... ; ..... ; .... ·v· ..... : .....
. .
0.8 ..... ! ..... ! v Process poles o lo o o o o . o o o o o o 0 . o o o o o
.
o 0
: ¢ PID zeroes
0.6
: c Pizero
0.4
0.2 ..... ; ..... ; ..... ; ..... ; ..... ; .. ~ ... : ...... : .... .
0 ........... D· ....•.....•.....•.....•.....•.....
.
.
.
.
-0.2 ···:·····:·····:··~···:··
-0.4
-0.6 ................................
0
0
I
I
•
0
0
0
-0.8
I I I I
-1 · · · · · · · · · · · · :· · · · · :· · · · · :· · · · ·V· · · · · · · · · ·
-0.4 -0.35 -0.3 -0.25 -0.2 -0.15 -0.1 -0.05 0
F1caURE 8-12 Poles of process and zeroes of PI and PID controller.