Page 219 - Practical Control Engineering a Guide for Engineers, Managers, and Practitioners

Distributed Processes 193

going to key on. The dynamics of the slave loop are considered to be
so much faster than those of the liquid temperature control loop that
they can be neglected. This master I slave configuration is a cascade
control structure and will be dealt with in Chap. 11.
At time zero, the step in the set point causes the proportional
component of the control algorithm to jump to 3.0 (which makes
sense because the proportional gain is 3.0). As the outlet temperature
starts to respond, the proportional component backs off. At t = 1.0 the
initial contents of the tube have passed through the exchanger.
Although there is a delay for the liquid to pass through the tube, all
of the liquid sees the step in the jacket temperature immediately so
there is no dead-time effect. For t > 1. 0 the tube will contain material
that has entered the exchanger after the set point was stepped and the
outlet temperature will back off slightly with an associated response
of the proportional component. All this time, the integral component
has been slowly working to bring the outlet temperature near the set
point. The reader can try other control gain combinations by modify-
ing the Matlab script that generated Fig. 7-11.
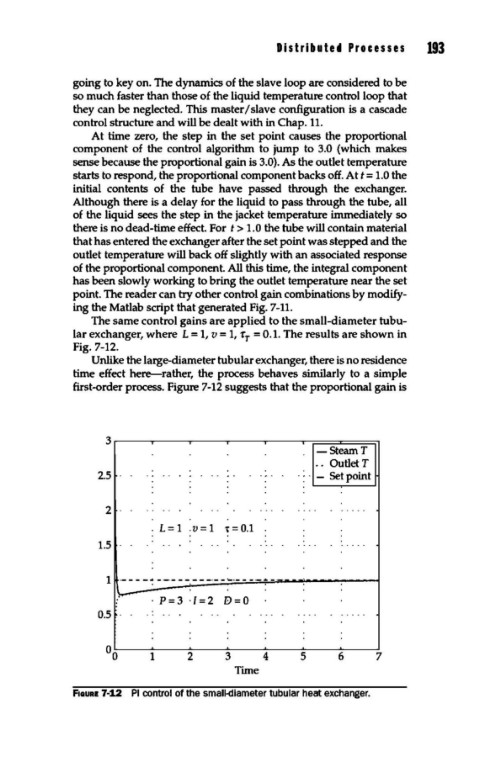
The same control gains are applied to the small-diameter tubu-
lar exchanger, where L = 1, v = 1, rr = 0.1. The results are shown in
Fig. 7-12.
Unlike the large-diameter tubular exchanger, there is no residence
time effect here-rather, the process behaves similarly to a simple
first-order process. Figure 7-12 suggests that the proportional gain is

3r---,---.----.----.----~==~==~
-Steam T
0
.. OutletT
2.5 0 : 0 - Set point

2
L = 1 ° v = 1 t = 0.1
1.5

1 --- - - ... - - -- -- --- - -·- - - • -
~0 0
o P = 3 I = 2 E> = 0
;· o
0.5

1 2 3 4 5 6 7
Time
F1aURE 7-12 PI control of the small-diameter tubular heat exchanger.