Page 106 - Radar Technology Encyclopedia

96 CONVOLUTION COORDINATES, radar

CONVOLUTION is defined as a function f (t) obtained from
y
two other functions, f (t) and f (t), by the following rule: x
1
2
¥
1 ò
×
(
ft () = f t()f t – t ) t
d
2
– ¥
The typical symbolic notation is
q sin f
ft () f t () f t ()Ä 2
=
1
The concept of convolution is widely used in the theory of
q f
spectral analysis of radar waveforms and digital signal pro- q cos f
cessing. The convolution theorem states that the Fourier
transform of the convolution of two functions is the product
z
of their individual Fourier transforms. This means that convo-
lution in the time domain can be carried out by multiplication
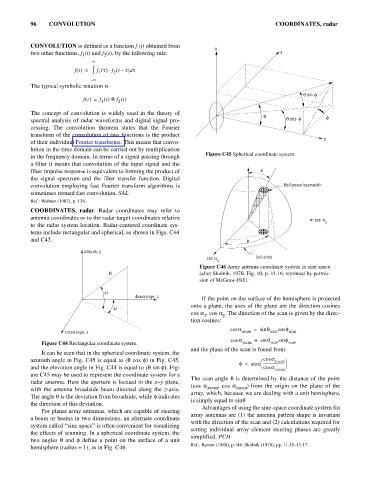
Figure C45 Spherical coordinate system.
in the frequency domain. In terms of a signal passing through
a filter it means that convolution of the input signal and the
filter impulse response is equivalent to forming the product of q
the signal spectrum and the filter transfer function. Digital
convolution employing fast Fourier transform algorithms is Half-power beamwidth
sometimes termed fast convolution. SAL
Ref.: Wehner (1987), p. 138.
COORDINATES, radar. Radar coordinates may refer to
antenna coordinates or to the radar target coordinates relative
cos a y
to the radar system location. Radar-centered coordinate sys-
tems include rectangular and spherical, as shown in Figs. C44
and C45. f

altitude, y
cos a Unit circle
x
Figure C46 Array antenna coordinate system in sine space
R (after Skolnik, 1970, Fig. 10, p. 11.16, reprinted by permis-
sion of McGraw-Hill).

el
downrange, z
If the point on the surface of the hemisphere is projected
onto a plane, the axes of the plane are the direction cosines
az
cos a , cos a The direction of the scan is given by the direc-
y.
x
tion cosines:
cos a = sin q cos f
crossrange, x xscan scan scan
cos a = sin q sin f
Figure C44 Rectangular coordinate system. yscan scan scan
and the plane of the scan is found from:
It can be seen that in the spherical coordinate system, the
azimuth angle in Fig. C45 is equal to (q cos f) in Fig. C45, æ cos a yscan ö
f = atan -----------------------
Fi
and the elevation angle in Fig. C44 is equal to (q sin f). - è cos a ø
g
xscan
ure C45 may be used to represent the coordinate system for a
i
The scan angle q s determined by the distance of the point
radar antenna. Here the aperture is located in the x-y plane,
(cos a xscan , cos a yscan
) from the origin on the plane of the
with the antenna broadside beam directed along the z-axis.
array, which, because we are dealing with a unit hemisphere,
The angle q is the deviation from broadside, while f indicates
is simply equal to sinq
the direction of this deviation.
Advantages of using the sine-space coordinate system for
For planar array antennas, which are capable of steering
array antennas are (1) the antenna pattern shape is invariant
a beam or beams in two dimensions, an alternate coordinate
with the direction of the scan and (2) calculations required for
system called “sine space” is often convenient for visualizing
setting individual array element steering phases are greatly
the effects of scanning. In a spherical coordinate system, the
simplified. PCH
two angles q and f define a point on the surface of a unit
Ref.: Barton (1988), p.146, Skolnik (1970), pp. 11.15–11.17.
hemisphere (radius = 1), as in Fig. C46.