Page 110 -

96 CHAPTER 4 Statistical analysis

As we mentioned before, nonparametric tests are not assumption free. The
Chi-squared test requires two assumptions that the data must satisfy in order to make
a valid judgment. First, the data points in the contingency table must be independent
from each other. In other words, one participant can only contribute one data point
in the contingency table. To give a more specific example, you cannot have a par-
ticipant that prefers both the mouse and the touchscreen. All the numbers presented
in Tables 4.25 and 4.26 have to be contributed by independent samples. Second, the
Chi-squared test does not work well when the sample is too small. It is generally
suggested that, to acquire a robust Chi-square, the total sample size needs to be 20 or
larger (Camilli and Hopkins, 1978).

4.8.2 OTHER NONPARAMETRIC TESTS
Many parametric tests have corresponding nonparametric alternatives. If you are
comparing data collected from two independent samples (e.g., data collected us-
ing a between-group design), the independent-samples t test can be used when the
parametric analysis assumptions are met. When the assumptions are not met, the
Mann-Whitney U test or the Wald-Wolfowitz runs test may be considered. If you are
comparing two sets of data collected from the same user group (e.g., data collected
using a within-group design), the paired-samples t test is typically adopted when
the assumptions are met. If not, the Wilcoxon signed-rank test can be used instead.
The following example illustrates the use of the Mann-Whitney U test. Suppose
you are evaluating two authentication techniques: the traditional alphanumeric pass-
word and an image-based password that contain several images preselected by the
user. You recruit two groups of participants. Each group uses one authentication tech-
nique to complete a number of login tasks. In addition to performance measures such
as task completion time, failed login tasks, and keystroke level data, you also ask the
participants to answer a questionnaire at the end of the study. Each participant rates
the general level of frustration when using the authentication technique through a
7-point Likert scale question (1 = least frustrated, 7 = most frustrated). Sample data for
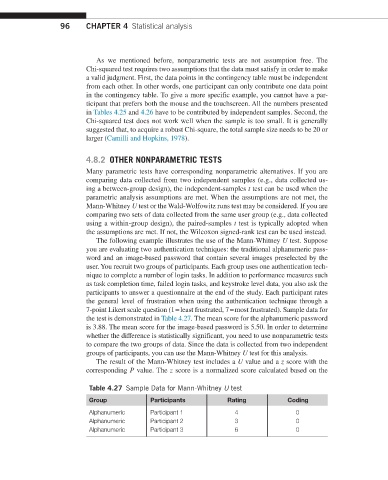
the test is demonstrated in Table 4.27. The mean score for the alphanumeric password
is 3.88. The mean score for the image-based password is 5.50. In order to determine
whether the difference is statistically significant, you need to use nonparametric tests
to compare the two groups of data. Since the data is collected from two independent
groups of participants, you can use the Mann-Whitney U test for this analysis.
The result of the Mann-Whitney test includes a U value and a z score with the
corresponding P value. The z score is a normalized score calculated based on the
Table 4.27 Sample Data for Mann-Whitney U test

Group Participants Rating Coding
Alphanumeric Participant 1 4 0
Alphanumeric Participant 2 3 0
Alphanumeric Participant 3 6 0