Page 227 - Schaum's Outline of Theory and Problems of Advanced Calculus

218 MULTIPLE INTEGRALS [CHAP. 9

Fig. 9-12
Note that the limits of integration for the region r can be constructed directly from the region r in the
0
xy plane without actually constructing the region r .In such case we use a grid as in Problem 9.6. The
0
coordinates ðu; vÞ are curvilinear coordinates, in this case called hyperbolic coordinates.
ðð q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
2
2
9.9. Evaluate x þ y dx dy, where r is the region in the xy plane bounded by x þ y ¼ 4 and
r
2
2
x þ y ¼ 9.
2
2
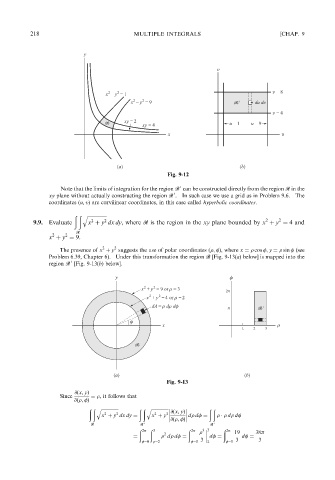
The presence of x þ y suggests the use of polar coordinates ð ; Þ, where x ¼ cos ; y ¼ sin (see
Problem 6.39, Chapter 6). Under this transformation the region r [Fig. 9-13(a)below] is mapped into the
region r [Fig. 9-13(b)below].
0

Fig. 9-13
Since @ðx; yÞ ¼ ,itfollows that
@ð ; Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ðð
ðð q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ðð q
@ðx; yÞ
2 2 x þ y 2 d d
2
x þ y dx dy ¼ d d ¼

@ð ; Þ
r r 0 r 0

ð 2 ð 3 ð 2 3 3 ð 2 19 38
2

¼ d d ¼ d ¼ d ¼ 3
¼0 ¼2 ¼0 3 2 ¼0 3