Page 375 - Schaum's Outline of Theory and Problems of Advanced Calculus

366 FOURIER INTEGRALS [CHAP. 14

f
F
Now suppose that g ¼ f and thus G ¼ F, where the bar symbolizes the complex conjugate function.
Then (15) takes the form
ð ð
1 1
2 2
j f ðuÞj du ¼ jFð Þj d ð16Þ
1 1
This is Parseval’s theorem for Fourier integrals.
Furthermore, if f and g are even functions, it can be shown that (15) reduces to the following
Parseval identities:
ð ð
1 1
F c ð Þ G c ð Þ d
f ðuÞ gðuÞ du ¼ ð17Þ
0 0
where F c and G c are the Fourier cosine transforms of f and g. If f and g are odd functions, the (15)
takes the form
ð ð
1 1
F s ð Þ G s ð Þ d
f ðuÞ gðuÞ du ¼ ð18Þ
0 0
where F s and G s are the Fourier sine transforms of f and g. (See Problem 14.3.)

Solved Problems

THE FOURIER INTEGRAL AND FOURIER TRANSFORMS

1 jxj < a
.
0 jxj > a
14.1. (a) Find the Fourier transform of f ðxÞ¼
(b) Graph f ðxÞ and its Fourier transform for a ¼ 3.
(a) The Fourier transform of f ðxÞ is

1 ð 1 i u 1 ð a i u 1 e i u a

f ðuÞ e ð1Þ e
ffiffiffiffiffiffi
Fð Þ¼ p ffiffiffiffiffiffi du ¼ p ffiffiffiffiffiffi du ¼ p 2 i
2 a a
2 1
2 sin a
1 e i a e i a r ffiffiffi
; 6¼ 0
¼ p ffiffiffiffiffiffi ¼
2 i
ffiffiffiffiffiffiffiffi
p
2= a.
For ¼ 0, we obtain Fð Þ¼
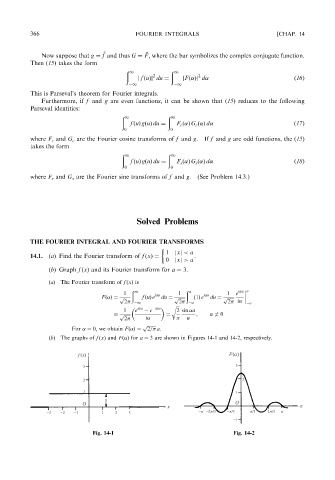
(b) The graphs of f ðxÞ and Fð Þ for a ¼ 3are shown in Figures 14-1 and 14-2, respectively.
f (x) F(α)
3 3
2 2
1 1
1
O O
x α
_ _ _ _ p _ 2p/3 _ p/3 p/3 2p/3 p
3 2 1 1 2 3
_
1
Fig. 14-1 Fig. 14-2