Page 129 - Schaum's Outline of Theory and Problems of Electric Circuits

WAVEFORMS AND SIGNALS
118
1 [CHAP. 6
hcos ð2 f 1 t þ 1 Þ cos ð2 f 2 t þ 2 Þi ¼ hcos ½2 ð f 1 þ f 2 Þt þð 1 þ 2 ފi
2
1
þ hcos ½2 ð f 1 f 2 Þt þð 1 2 ފi ¼ 0
2
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 1 2 2 1 2 2
Therefore, V eff ¼ ðV 1 þ V 2 Þ and V eff ¼ ðV þ V Þ:
2 2 1 2
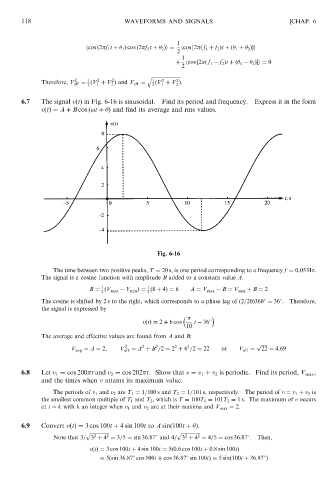
6.7 The signal vðtÞ in Fig. 6-16 is sinusoidal. Find its period and frequency. Express it in the form
vðtÞ¼ A þ B cos ð!t þ Þ and find its average and rms values.

Fig. 6-16

The time between two positive peaks, T ¼ 20 s, is one period corresponding to a frequency f ¼ 0:05 Hz.
The signal is a cosine function with amplitude B added to a constant value A.
1
1
B ¼ ðV max V min Þ¼ ð8 þ 4Þ¼ 6 A ¼ V max B ¼ V min þ B ¼ 2
2 2
The cosine is shifted by 2 s to the right, which corresponds to a phase lag of ð2=20Þ3608 ¼ 368. Therefore,
the signal is expressed by

vðtÞ¼ 2 þ 6 cos t 368
10
The average and effective values are found from A and B:
p ffiffiffiffiffi
2
2
2
2
2
V avg ¼ A ¼ 2; V eff ¼ A þ B =2 ¼ 2 þ 6 =2 ¼ 22 or V eff ¼ 22 ¼ 4:69
6.8 Let v 1 ¼ cos 200 t and v 2 ¼ cos 202 t. Show that v ¼ v 1 þ v 2 is periodic. Find its period, V max ,
and the times when v attains its maximum value.
The periods of v 1 and v 2 are T 1 ¼ 1=100 s and T 2 ¼ 1=101 s, respectively. The period of v ¼ v 1 þ v 2 is
the smallest common multiple of T 1 and T 2 , which is T ¼ 100T 1 ¼ 101T 2 ¼ 1 s. The maximum of v occurs
at t ¼ k with k an integer when v 1 and v 2 are at their maxima and V max ¼ 2.

6.9 Convert vðtÞ¼ 3 cos 100t þ 4 sin 100t to A sinð100t þ Þ.
p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
2
2
Note that 3= 3 þ 4 ¼ 3=5 ¼ sin 36:878 and 4= 3 þ 4 ¼ 4=5 ¼ cos 36:878. Then,
vðtÞ¼ 3 cos 100t þ 4 sin 100t ¼ 5ð0:6 cos 100t þ 0:8 sin 100tÞ
¼ 5ðsin 36:878 cos 100t þ cos 36:878 sin 100tÞ¼ 5 sinð100t þ 36:878Þ