Page 126 - Schaum's Outline of Theory and Problems of Electric Circuits
P. 126

CHAP. 6]
               (a) We have                    WAVEFORMS AND SIGNALS                                  115
                                   v R ¼ Ri ¼ RI 0 e  at  cos !t
                                         di       at
                                   v L ¼ L  ¼ LI 0 e  ða cos !t þ ! sin !tÞ
                                         dt
                                  v RL ¼ v R þ v L ¼ I 0 e  at ½ðR   LaÞ cos !t   L! sin !tŠ¼ V 0 e  at  cos ð!t þ  Þ
                                            q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
                                                    2   2 2                1
                   where              V 0 ¼ I 0 ðR   LaÞ þ L !  and    ¼ tan ½L!=ðR   Laފ           (39)
               (b) Substituting the given data into (39), V 0 ¼ 18:75 V and   ¼ 39:88. Current i and voltage v RL are then given by
                                            2t                         2t
                                      i ¼ 3e  cos 40t  and  v RL ¼ 18:75e  cos ð40t þ 39:88Þ
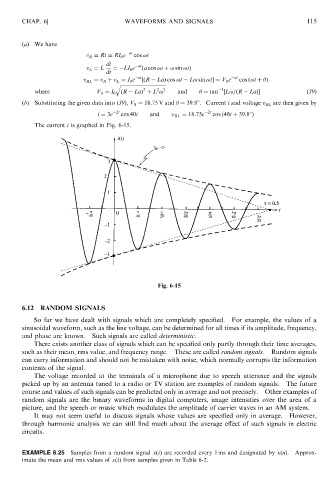
                   The current i is graphed in Fig. 6-15.





























                                                        Fig. 6-15


               6.12  RANDOM SIGNALS
                   So far we have dealt with signals which are completely specified.  For example, the values of a
               sinusoidal waveform, such as the line voltage, can be determined for all times if its amplitude, frequency,
               and phase are known.  Such signals are called deterministic.
                   There exists another class of signals which can be specified only partly through their time averages,
               such as their mean, rms value, and frequency range.  These are called random signals.  Random signals
               can carry information and should not be mistaken with noise, which normally corrupts the information
               contents of the signal.
                   The voltage recorded at the terminals of a microphone due to speech utterance and the signals
               picked up by an antenna tuned to a radio or TV station are examples of random signals.  The future
               course and values of such signals can be predicted only in average and not precisely.  Other examples of
               random signals are the binary waveforms in digital computers, image intensities over the area of a
               picture, and the speech or music which modulates the amplitude of carrier waves in an AM system.
                   It may not seem useful to discuss signals whose values are specified only in average. However,
               through harmonic analysis we can still find much about the average effect of such signals in electric
               circuits.


               EXAMPLE 6.25 Samples from a random signal xðtÞ are recorded every 1 ms and designated by xðnÞ.  Approx-
               imate the mean and rms values of xðtÞ from samples given in Table 6-2.
   121   122   123   124   125   126   127   128   129   130   131