Page 121 - Schaum's Outline of Theory and Problems of Electric Circuits

WAVEFORMS AND SIGNALS
[CHAP. 6
110
EXAMPLE 6.15 If the switch in Fig. 6-8(a) is moved to position 2 at t ¼ 0 and then moved back to position 1 at
t ¼ 5 s, express v AB using the step function.
v AB ¼ V 0 ½uðtÞ uðt 5ފ

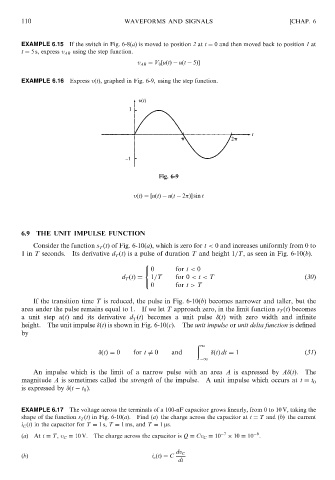
EXAMPLE 6.16 Express vðtÞ, graphed in Fig. 6-9, using the step function.

Fig. 6-9

vðtÞ¼½uðtÞ uðt 2 ފ sin t

6.9 THE UNIT IMPULSE FUNCTION
Consider the function s T ðtÞ of Fig. 6-10(a), which is zero for t < 0 and increases uniformly from 0 to
1in T seconds. Its derivative d T ðtÞ is a pulse of duration T and height 1=T, as seen in Fig. 6-10(b).
8
< 0 for t < 0
d T ðtÞ¼ 1=T for 0 < t < T ð30Þ
:
0 for t > T
If the transition time T is reduced, the pulse in Fig. 6-10(b) becomes narrower and taller, but the
area under the pulse remains equal to 1. If we let T approach zero, in the limit function s ðtÞ becomes
T
a unit step uðtÞ and its derivative d T ðtÞ becomes a unit pulse ðtÞ with zero width and infinite
height. The unit impulse ðtÞ is shown in Fig. 6-10(c). The unit impulse or unit delta function is defined
by
ð
1
ðtÞ¼ 0 for t 6¼ 0 and ðtÞ dt ¼ 1 ð31Þ
1

An impulse which is the limit of a narrow pulse with an area A is expressed by A ðtÞ. The
magnitude A is sometimes called the strength of the impulse. A unit impulse which occurs at t ¼ t 0
is expressed by ðt t 0 Þ.

EXAMPLE 6.17 The voltage across the terminals of a 100-nF capacitor grows linearly, from 0 to 10 V, taking the
shape of the function s T ðtÞ in Fig. 6-10(a). Find (a) the charge across the capacitor at t ¼ T and (b) the current
i C ðtÞ in the capacitor for T ¼ 1s, T ¼ 1 ms, and T ¼ 1 ms.
6
(a)At t ¼ T, v C ¼ 10 V. The charge across the capacitor is Q ¼ Cv C ¼ 10 7 10 ¼ 10 .

dv C
ðbÞ i c ðtÞ¼ C
dt