Page 161 - Schaum's Outline of Theory and Problems of Electric Circuits

FIRST-ORDER CIRCUITS
150
From the assumption qð0Þ¼ 0 and the condition [CHAP. 7

dq 20 V
þ
ið0 Þ¼ ¼ ¼ 40 mA
dt 0 þ 500
we find that A ¼ B ¼ 10 mC, or
q ¼ 10ð1 e 4000t Þ ðmCÞ ð0 t Þ ð20Þ
1
From (20), qð Þ¼ 10ð1 e Þ mC; and we know that qð1Þ ¼ ð0:5 mFÞð 40 VÞ¼ 20 mC.
Hence, q, is determined for t as
ðt Þ= 4000t
q ¼½qð Þ qð1ފe þ qð1Þ ¼ 71:55e 20 ðmCÞ ð21Þ
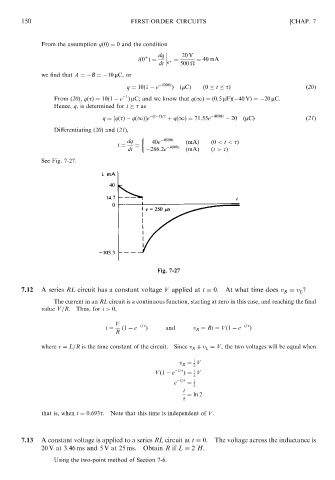
Differentiating (20) and (21),

dq 40e 4000t ðmAÞ ð0 < t < Þ
i ¼ ¼ 4000t
dt 286:2e ðmAÞ ðt > Þ
See Fig. 7-27.

Fig. 7-27

7.12 A series RL circuit has a constant voltage V applied at t ¼ 0. At what time does v R ¼ v L ?

The current in an RL circuit is a continuous function, starting at zero in this case, and reaching the final
value V=R. Thus, for t > 0,

V t= t=
i ¼ ð1 e Þ and v R ¼ Ri ¼ Vð1 e Þ
R
where ¼ L=R is the time constant of the circuit. Since v R þ v L ¼ V, the two voltages will be equal when

1
v R ¼ V
2
1
Vð1 e t= Þ¼ V
2
e t= ¼ 1
2
t
¼ ln 2

that is, when t ¼ 0:693 . Note that this time is independent of V.

7.13 A constant voltage is applied to a series RL circuit at t ¼ 0. The voltage across the inductance is
20 V at 3.46 ms and 5 V at 25 ms. Obtain R if L ¼ 2 H.
Using the two-point method of Section 7-6.