Page 59 - Schaum's Outline of Theory and Problems of Electric Circuits

ANALYSIS METHODS
48

Fig. 4-17 [CHAP. 4

KVL and KCL give:
I 2 ð12Þ¼ I 3 ð6Þ ð10Þ
I 2 ð12Þ¼ I 4 ð12Þ ð11Þ
60 ¼ I 1 ð7Þþ I 2 ð12Þ ð12Þ
I 1 ¼ I 2 þ I 3 þ I 4 ð13Þ
Substituting (10) and (11)in(13),

I 1 ¼ I 2 þ 2I 2 þ I 2 ¼ 4I 2 ð14Þ
Now (14) is substituted in (12):
1
60 ¼ I 1 ð7Þþ I 1 ð12Þ¼ 10I 1 or I 1 ¼ 6A
4

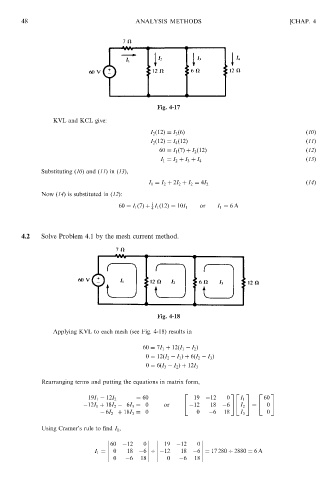
4.2 Solve Problem 4.1 by the mesh current method.

Fig. 4-18

Applying KVL to each mesh (see Fig. 4-18) results in

60 ¼ 7I 1 þ 12ðI 1 I 2 Þ
0 ¼ 12ðI 2 I 1 Þþ 6ðI 2 I 3 Þ
0 ¼ 6ðI 3 I 2 Þþ 12I 3
Rearranging terms and putting the equations in matrix form,
2 32 3 2 3
¼ 60 19 12 0 60
19I 1 12I 2 I 1
4
12I 1 þ 18I 2 6I 3 ¼ 0 or 4 12 18 6 5 I 2 5 ¼ 4 0 5
6I 2 þ 18I 3 ¼ 0 0 6 18 I 3 0
Using Cramer’s rule to find I 1 ,

60 12 0 19 12 0

I 1 ¼ 0 18 6 12 18 6 ¼ 17 280 2880 ¼ 6A

0 6 18 0 6 18