Page 84 - Schaum's Outline of Theory and Problems of Electric Circuits

AMPLIFIERS AND OPERATIONAL AMPLIFIER CIRCUITS
73
CHAP. 5]
The gain v 2 =v 1 is positive and greater than or equal to one. The input resistance of the circuit is infinite
as the op amp draws no current.

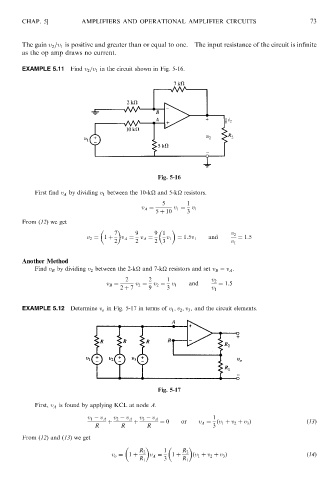
EXAMPLE 5.11 Find v 2 =v 1 in the circuit shown in Fig. 5-16.

Fig. 5-16

First find v A by dividing v 1 between the 10-k
and 5-k
resistors.
5 1
v A ¼ v 1 ¼ v 1
5 þ 10 3
From (12) we get

7 9 9 1 v 2
v 2 ¼ 1 þ v A ¼ v A ¼ v 1 ¼ 1:5v 1 and ¼ 1:5
2 2 2 3 v 1

Another Method
Find v B by dividing v 2 between the 2-k
and 7-k
resistors and set v B ¼ v A .
2 2 1 v 2
v B ¼ v 2 ¼ v 2 ¼ v 1 and ¼ 1:5
2 þ 7 9 3 v 1

EXAMPLE 5.12 Determine v o in Fig. 5-17 in terms of v 1 ; v 2 ; v 3 ; and the circuit elements.

Fig. 5-17

First, v A is found by applying KCL at node A.

v 1 v A v 2 v A v 3 v A 1
þ þ ¼ 0 or v A ¼ ðv 1 þ v 2 þ v 3 Þ ð13Þ
R R R 3
From (12) and (13) we get

R 2 1 R 2
v o ¼ 1 þ v A ¼ 1 þ ðv 1 þ v 2 þ v 3 Þ ð14Þ
R 1 3 R 1