Page 137 - Science at the nanoscale

RPS: PSP0007 - Science-at-Nanoscale
8:11
June 9, 2009
6.2. Electron Transport Properties in Low Dimensional Systems
5
conductance (G 0 )
4
3
2
1
0
0 1000 2000 3000
depth (nm)
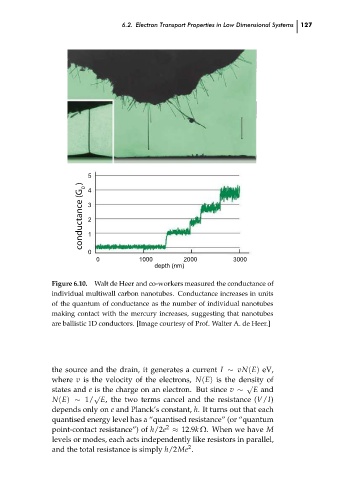
Figure 6.10.
Walt de Heer and co-workers measured the conductance of
individual multiwall carbon nanotubes. Conductance increases in units
of the quantum of conductance as the number of individual nanotubes
making contact with the mercury increases, suggesting that nanotubes
are ballistic 1D conductors. [Image courtesy of Prof. Walter A. de Heer.]
the source and the drain, it generates a current I ∼ vN(E) eV, 127 ch06
where v is the velocity of the electrons, N(E) is the density of
√
states and e is the charge on an electron. But since v ∼ E and
√
N(E) ∼ 1/ E, the two terms cancel and the resistance (V/I)
depends only on e and Planck’s constant, h. It turns out that each
quantised energy level has a “quantised resistance” (or “quantum
2
point-contact resistance”) of h/2e ≈ 12.9k Ω. When we have M
levels or modes, each acts independently like resistors in parallel,
2
and the total resistance is simply h/2Me .