Page 285 - Separation process engineering

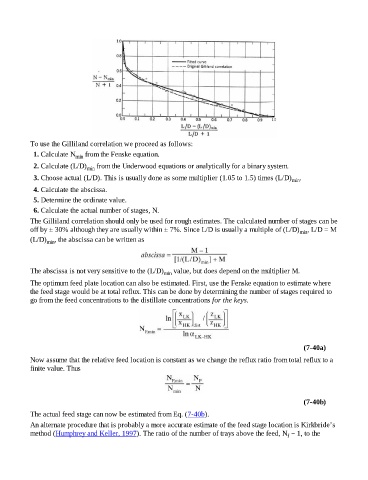
To use the Gilliland correlation we proceed as follows:

1. Calculate N min from the Fenske equation.

2. Calculate (L/D) min from the Underwood equations or analytically for a binary system.

3. Choose actual (L/D). This is usually done as some multiplier (1.05 to 1.5) times (L/D) min .

4. Calculate the abscissa.
5. Determine the ordinate value.

6. Calculate the actual number of stages, N.
The Gilliland correlation should only be used for rough estimates. The calculated number of stages can be
off by ± 30% although they are usually within ± 7%. Since L/D is usually a multiple of (L/D) min , L/D = M

(L/D) min , the abscissa can be written as

The abscissa is not very sensitive to the (L/D) min value, but does depend on the multiplier M.

The optimum feed plate location can also be estimated. First, use the Fenske equation to estimate where
the feed stage would be at total reflux. This can be done by determining the number of stages required to
go from the feed concentrations to the distillate concentrations for the keys.

(7-40a)

Now assume that the relative feed location is constant as we change the reflux ratio from total reflux to a
finite value. Thus

(7-40b)

The actual feed stage can now be estimated from Eq. (7-40b).

An alternate procedure that is probably a more accurate estimate of the feed stage location is Kirkbride’s
method (Humphrey and Keller, 1997). The ratio of the number of trays above the feed, N − 1, to the
f