Page 77 - Separation process principles 2

42 Chapter 2 Thermodynamics of Separation Operations

100 - I I 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2.5 NONIDEAL THERMODYNAMIC
- -
- PROPERTY MODELS
- 0 Experimental data I
Unlike the equations of Table 2.1, which are universally
applicable to all pure substances and mixtures, whether ideal
Temperature 250°F
- or nonideal, no universal equations are available for com-
puting, for nonideal mixtures, values of thermodynamic
properties such as density, enthalpy, entropy, fugacities, and
activity coefficients as functions of temperature, pressure,
and phase composition. Instead, two types of models are
used: (1) P-V-T equation-of-state models and (2) activity
coefficient or free-energy models. These are based on cons-
titutive equations because they depend on the constitution or
nature of the components in the mixture.
-
3
-
- P-V-T Equation-of-State Models
-
-
The first type of model is a relationship between molar vol-
-
ume (or density), temperature, and pressure, usually referred
to as a P-V-Tequation of state. A large number of such equa-
tions have been proposed, mostly for the vapor phase. The
simplest is the ideal-gas law, which applies only at low pres-
sures or high temperatures because it neglects the volume
occupied by the molecules and intermolecular forces among
the molecules. All other equations of state attempt to correct
for these two deficiencies. The equations of state that are
most widely used by chemical engineers are listed in
.01 l I I 1 1 1 1 1 1 1 I I I I I I I1 Table 2.5. These and other equations of state are discussed in
100 1000 10,000 some detail by Poling et al. [ll].
Pressure, psia Not included in Table 2.5 is the van der Waals equation,
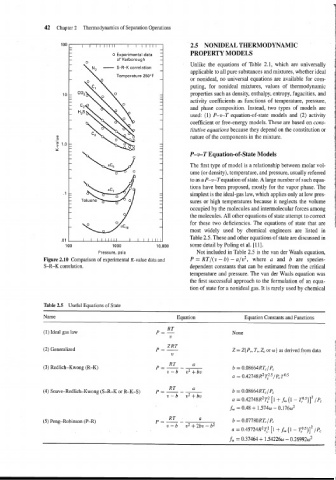
Figure 2.10 Comparison of experimental K-value data and P = RT/(v - b) - a/v2, where a and b are species-
S-R-K correlation. dependent constants that can be estimated from the critical
temperature and pressure. The van der Waals equation was
the first successful approach to the formulation of an equa-
tion of state for a nonideal gas. It is rarely used by chemical

Table 2.5 Useful Equations of State
Name Equation Equation Constants and Functions

RT
(1) Ideal gas law p=- None
v
ZRT
(2) Generalized p=- Z = Z{P,, T,, Zc or w] as derived from data
v
RT a
(3) Redlich-Kwong (R-K) p=--- b = 0.08664RTc/Pc
v-b v2+bv
a = 0.42748~~~:.~/ P~T~.~
R T a
(4) Soave-Redlich-Kwong (S-R-K or R-K-S) p=--- b = 0.08664RTc/Pc
v-b v2+bv
[l
a = 0.42748~~~: + fw (1 - T,D~)]? /PC
fw = 0.48 + 1.574~ - 0.176w2
RT a
(5) Peng-Robinson (P-R) P=-- b = 0.07780RTc/Pc
V-b v2+2bv-b2
[l
a = 0.45724~~~: + fw (1 - TP 5)]2 /PC
fw = 0.37464 + 1.54226" - 0.2699202