Page 321 - Shigley's Mechanical Engineering Design

bud29281_ch06_265-357.qxd 12/11/2009 4:56 pm Page 296 pinnacle 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

296 Mechanical Engineering Design
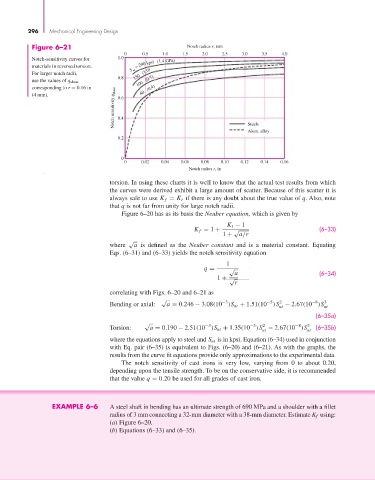
Figure 6–21 Notch radius r, mm
0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
Notch-sensitivity curves for 1.0
materials in reversed torsion. = 200 kpsi (1.4 GPa)
S ut
For larger notch radii, 150 (1.0)
0.8
use the values of q shear 100 (0.7)
corresponding to r = 0.16 in 60 (0.4)
Notch sensitivity q shear 0.4
(4 mm). 0.6

Steels
Alum. alloy
0.2

0
0 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16
Notch radius r, in
torsion. In using these charts it is well to know that the actual test results from which
the curves were derived exhibit a large amount of scatter. Because of this scatter it is
always safe to use K f = K t if there is any doubt about the true value of q. Also, note
that q is not far from unity for large notch radii.
Figure 6–20 has as its basis the Neuber equation, which is given by
K t − 1
K f = 1 + √ (6–33)
1 + a/r
√
where a is defined as the Neuber constant and is a material constant. Equating
Eqs. (6–31) and (6–33) yields the notch sensitivity equation
1
q = √
a (6–34)
1 + √
r
correlating with Figs. 6–20 and 6–21 as
√ −3 −5 2 −8 3
Bending or axial: a = 0.246 − 3.08(10 )S ut + 1.51(10 )S − 2.67(10 )S ut
ut
(6–35a)
√ −3 −5 2 −8 3
Torsion: a = 0.190 − 2.51(10 )S ut + 1.35(10 )S − 2.67(10 )S ut (6–35b)
ut
where the equations apply to steel and S ut is in kpsi. Equation (6–34) used in conjunction
with Eq. pair (6–35) is equivalent to Figs. (6–20) and (6–21). As with the graphs, the
results from the curve fit equations provide only approximations to the experimental data.
The notch sensitivity of cast irons is very low, varying from 0 to about 0.20,
depending upon the tensile strength. To be on the conservative side, it is recommended
that the value q = 0.20 be used for all grades of cast iron.

EXAMPLE 6–6 A steel shaft in bending has an ultimate strength of 690 MPa and a shoulder with a fillet
radius of 3 mm connecting a 32-mm diameter with a 38-mm diameter. Estimate K f using:
(a) Figure 6–20.
(b) Equations (6–33) and (6–35).