Page 431 - Shigley's Mechanical Engineering Design

bud29281_ch07_358-408.qxd 12/8/09 12:52PM Page 406 ntt 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

406 Mechanical Engineering Design

100
100
A B

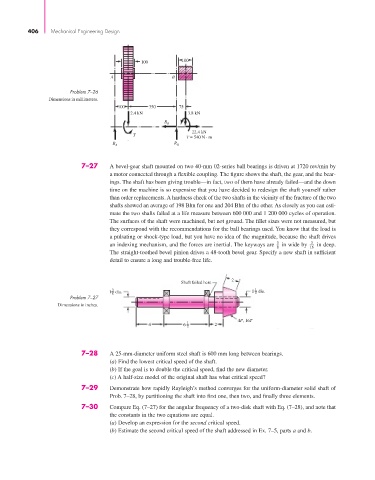
Problem 7–26
Dimensions in millimeters.
100 350 75
2.4 kN 3.8 kN
R B
22.4 kN
T
T = 540 N . m
R
R A
B
7–27 A bevel-gear shaft mounted on two 40-mm 02-series ball bearings is driven at 1720 rev/min by
a motor connected through a flexible coupling. The figure shows the shaft, the gear, and the bear-
ings. The shaft has been giving trouble—in fact, two of them have already failed—and the down
time on the machine is so expensive that you have decided to redesign the shaft yourself rather
than order replacements. A hardness check of the two shafts in the vicinity of the fracture of the two
shafts showed an average of 198 Bhn for one and 204 Bhn of the other. As closely as you can esti-
mate the two shafts failed at a life measure between 600 000 and 1 200 000 cycles of operation.
The surfaces of the shaft were machined, but not ground. The fillet sizes were not measured, but
they correspond with the recommendations for the ball bearings used. You know that the load is
a pulsating or shock-type load, but you have no idea of the magnitude, because the shaft drives
an indexing mechanism, and the forces are inertial. The keyways are 3 in wide by 3 in deep.
8 16
The straight-toothed bevel pinion drives a 48-tooth bevel gear. Specify a new shaft in sufficient
detail to ensure a long and trouble-free life.

2
Shaft failed here
3 1
1 dia. 1 dia.
2
8
Problem 7–27
Dimensions in inches.
4P, 16T
1
4 6 2 2

7–28 A 25-mm-diameter uniform steel shaft is 600 mm long between bearings.
(a) Find the lowest critical speed of the shaft.
(b) If the goal is to double the critical speed, find the new diameter.
(c) A half-size model of the original shaft has what critical speed?
7–29 Demonstrate how rapidly Rayleigh’s method converges for the uniform-diameter solid shaft of
Prob. 7–28, by partitioning the shaft into first one, then two, and finally three elements.
7–30 Compare Eq. (7–27) for the angular frequency of a two-disk shaft with Eq. (7–28), and note that
the constants in the two equations are equal.
(a) Develop an expression for the second critical speed.
(b) Estimate the second critical speed of the shaft addressed in Ex. 7–5, parts a and b.