Page 258 - Soil and water contamination, 2nd edition

Chemical transformation 245

Third, use Equation (13.9) to estimate the retardation factor :
1675 3
R 1 . 1 614 10 10
f
3 . 0
Thus, the migration velocity of the 1,4-dichlorobenzene plume is 9.9 times less than the
average groundwater flow velocity:
u x 50 5 m y -1
R 10
f

So far in this section, we have assumed equilibrium between the dissolved and adsorbed
phases . However, if the reaction rates are slow compared to the transport rate, reaction

kinetics has to be taken into account. For example, in surface waters, it takes usually several

hours to days before equilibrium is reached between the solute and the adsorbed phase ,
because the mass of solids is usually small compared to the water volume. During this
time the solution is moved over a considerable distance due to water flow, so it is therefore
necessary to account for the sorption kinetics.
In adsorption –desorption reactions, the rate of change in the solute concentration is the
sum of the rate of removal by adsorption and the rate of production by desorption (Stumm
and Morgan, 1996). If both the adsorption and desorption reactions are simulated using

first-order kinetics , the differential equation is:
dC w k C k C (13.11)
dt ads w des s
-1
-3
-1
where k = adsorption rate constant [T ] and k = desorption rate constant [M L T ]. At
ads des
equilibrium, the net change of C equals zero, so:
w
dC w
0 k ads C w k des C s 0 (13.12)
dt
0
5

10

15
Depth
20

25

30
6642 6642 6642 35
0 50 100 150 200 250 300 350
Horizontal distance
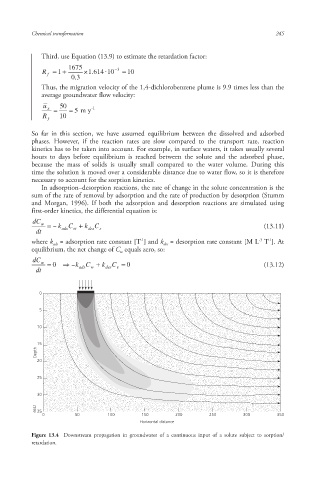
Figure 13.4 Downstream propagation in groundwater of a continuous input of a solute subject to sorption /
retardation.

10/1/2013 6:45:11 PM
Soil and Water.indd 257 10/1/2013 6:45:11 PM
Soil and Water.indd 257