Page 111 - Statistics and Data Analysis in Geology

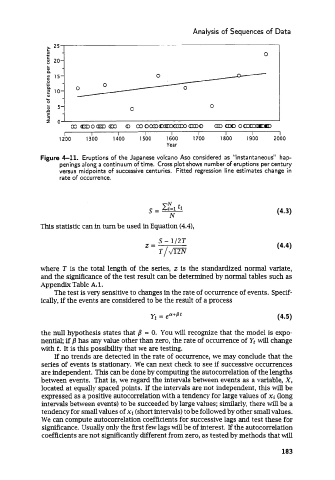
Analysis of Sequences of Data

5 25
0
Y
; 20-
L
0)
n
2 15- 0
.-
0
o.
Y
2 10-
01
L
k
n 5- 0 0
5
2 0

This statistic can in turn be used in Equation (4.4),
S - 1/2T
Z= (4.4)
T/rn

where T is the total length of the series, z is the standardized normal variate,
and the significance of the test result can be determined by normal tables such as
Appendix Table A. 1.
The test is very sensitive to changes in the rate of occurrence of events. Specif-
ically, if the events are considered to be the result of a process

yt = p+Bt (4.5)

the null hypothesis states that fi = 0. You will recognize that the model is expo-
nential; if fi has any value other than zero, the rate of occurrence of Yt will change
with t. It is this possibility that we are testing.
If no trends are detected in the rate of occurrence, we may conclude that the
series of events is stationary. We can next check to see if successive occurrences
are independent. This can be done by computing the autocorrelation of the lengths
between events. That is, we regard the intervals between events as a variable, X,
located at equally spaced points. If the intervals are not independent, this will be
expressed as a positive autocorrelation with a tendency for large values of Xi (long
intervals between events) to be succeeded by large values; similarly, there will be a
tendency for small values of xi (short intervals) to be followed by other smallvalues.
We can compute autocorrelation coefficients for successive lags and test these for
significance. Usually only the first few lags will be of interest. If the autocorrelation
coefficients are not significantly different from zero, as tested by methods that will

183