Page 202 - Statistics for Environmental Engineers

l1592_frame_Ch23 Page 202 Tuesday, December 18, 2001 2:44 PM

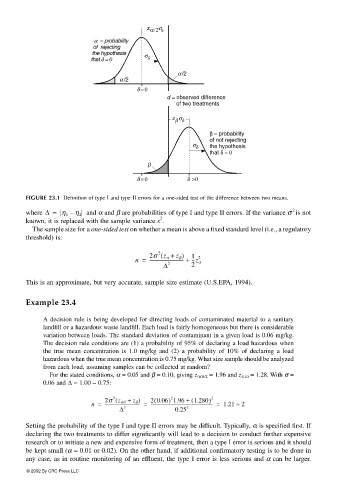
σ
z α/2 δ
α = probability
of rejecting
the hypothesis σ
that δ = 0 δ
α/2
α/2
δ = 0
d = observed difference

of two treatments
z σ
βδ
β = probability
of not rejecting
σ δ the hypothesis
that δ = 0
β
δ = 0 δ > 0

FIGURE 23.1 Definition of type I and type II errors for a one-sided test of the difference between two means.
where ∆ = η 1 η 2 and α and β are probabilities of type I and type II errors. If the variance σ is not
2
–
2
known, it is replaced with the sample variance s .
The sample size for a one-sided test on whether a mean is above a fixed standard level (i.e., a regulatory
threshold) is:
2σ z α +( z β )
2
n = ------------------------------ + 1 2
---z α
∆ 2 2
This is an approximate, but very accurate, sample size estimate (U.S.EPA, 1994).

Example 23.4

A decision rule is being developed for directing loads of contaminated material to a sanitary
landfill or a hazardous waste landfill. Each load is fairly homogeneous but there is considerable
variation between loads. The standard deviation of contaminant in a given load is 0.06 mg/kg.
The decision rule conditions are (1) a probability of 95% of declaring a load hazardous when
the true mean concentration is 1.0 mg/kg and (2) a probability of 10% of declaring a load
hazardous when the true mean concentration is 0.75 mg/kg. What size sample should be analyzed
from each load, assuming samples can be collected at random?
For the stated conditions, α = 0.05 and β = 0.10, giving z 0.05/2 = 1.96 and z 0.10 = 1.28. With σ =
0.06 and ∆ = 1.00 – 0.75:

2σ z α/2 +( z β ) 2 0.06) 1.96 + ( 1.280) 2
(
2
2
n = -------------------------------- = ---------------------------------------------------------- = 1.21 ≈ 2
∆ 2 0.25 2
Setting the probability of the type I and type II errors may be difficult. Typically, α is specified first. If
declaring the two treatments to differ significantly will lead to a decision to conduct further expensive
research or to initiate a new and expensive form of treatment, then a type I error is serious and it should
be kept small (α = 0.01 or 0.02). On the other hand, if additional confirmatory testing is to be done in
any case, as in routine monitoring of an effluent, the type I error is less serious and α can be larger.
© 2002 By CRC Press LLC