Page 78 - Sustainability in the Process Industry Integration and Optimization

P r o c e s s I n t e g r a t i o n f o r I m p r ov i n g E n e r g y E f f i c i e n c y 55

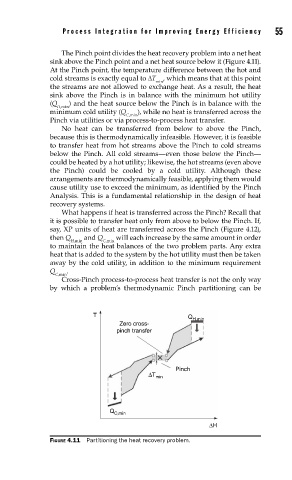
The Pinch point divides the heat recovery problem into a net heat
sink above the Pinch point and a net heat source below it (Figure 4.11).
At the Pinch point, the temperature difference between the hot and
cold streams is exactly equal to ΔT , which means that at this point
min
the streams are not allowed to exchange heat. As a result, the heat
sink above the Pinch is in balance with the minimum hot utility
(Q ) and the heat source below the Pinch is in balance with the
H,min
minimum cold utility (Q ), while no heat is transferred across the
C,min
Pinch via utilities or via process-to-process heat transfer.
No heat can be transferred from below to above the Pinch,
because this is thermodynamically infeasible. However, it is feasible
to transfer heat from hot streams above the Pinch to cold streams
below the Pinch. All cold streams—even those below the Pinch—
could be heated by a hot utility; likewise, the hot streams (even above
the Pinch) could be cooled by a cold utility. Although these
arrangements are thermodynamically feasible, applying them would
cause utility use to exceed the minimum, as identified by the Pinch
Analysis. This is a fundamental relationship in the design of heat
recovery systems.
What happens if heat is transferred across the Pinch? Recall that
it is possible to transfer heat only from above to below the Pinch. If,
say, XP units of heat are transferred across the Pinch (Figure 4.12),
then Q and Q will each increase by the same amount in order
H,min C,min
to maintain the heat balances of the two problem parts. Any extra
heat that is added to the system by the hot utility must then be taken
away by the cold utility, in addition to the minimum requirement
Q .
C,min
Cross-Pinch process-to-process heat transfer is not the only way
by which a problem’s thermodynamic Pinch partitioning can be

T Q H,min
Zero cross-
pinch transfer

Pinch
ΔT
min

Q C,min
ΔH

FIGURE 4.11 Partitioning the heat recovery problem.