Page 83 - Sustainability in the Process Industry Integration and Optimization

60 Cha p te r F o u r

the topmost heat flow, after which the cascading described in Step 4
is repeated. The resulting heat cascade is guaranteed to be feasible
and provides numerical heat recovery targets for the problem. The
topmost heat flow represents the minimum hot utility, the bottommost
heat flow represents the minimum cold utility, and the TB with zero
heat flow represents the location of the (heat recovery) Pinch. It is
often possible to obtain more than one zero-flow temperature
boundary, each representing a separate Pinch point.

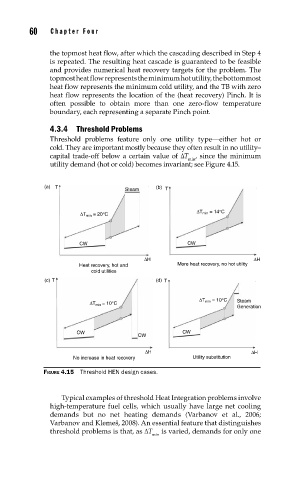
4.3.4 Threshold Problems
Threshold problems feature only one utility type—either hot or
cold. They are important mostly because they often result in no utility–
capital trade-off below a certain value of ΔT , since the minimum
min
utility demand (hot or cold) becomes invariant; see Figure 4.15.

(a) T (b)
Steam T

ΔT min = 14°C
ΔT min = 20°C

CW CW
ΔH ΔH
Heat recovery, hot and More heat recovery, no hot utility
cold utilities
(c) T (d) T

ΔT min = 10°C Steam
ΔT min = 10°C
Generation

CW CW
CW
ΔH ΔH
No increase in heat recovery Utility substitution
FIGURE 4.15 Threshold HEN design cases.

Typical examples of threshold Heat Integration problems involve
high-temperature fuel cells, which usually have large net cooling
demands but no net heating demands (Varbanov et al., 2006;
Varbanov and Klemeš, 2008). An essential feature that distinguishes
threshold problems is that, as ΔT is varied, demands for only one
min