Page 180 - The Combined Finite-Discrete Element Method

CONSTANT STRAIN TRIANGLE FINITE ELEMENT 163

Rotated (intermediate)
configuration
Deformed
y (rotated and
stretched)
configuration

Initial configuration
x

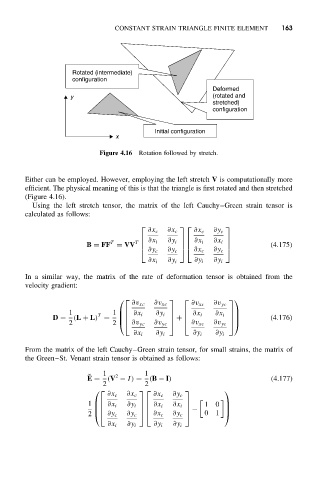
Figure 4.16 Rotation followed by stretch.

Either can be employed. However, employing the left stretch V is computationally more
efficient. The physical meaning of this is that the triangle is first rotated and then stretched
(Figure 4.16).
Using the left stretch tensor, the matrix of the left Cauchy–Green strain tensor is
calculated as follows:

   
∂x c ∂x c ∂x c ∂y c
T

B = FF = VV T  ∂x i ∂y i   ∂x i ∂x i  (4.175)
 

∂y c ∂y c
   ∂x c ∂y c 
∂x i ∂y i ∂y i ∂y i
In a similar way, the matrix of the rate of deformation tensor is obtained from the
velocity gradient:
   
∂v xc ∂v xc ∂v xc ∂v yc
1 T 1  ∂x i ∂y i   ∂x i ∂x i 
D = (L + L) =   +   (4.176)
2 2  ∂v yc ∂v yc   ∂v xc ∂v yc 
∂x i ∂y i ∂y i ∂y i
From the matrix of the left Cauchy–Green strain tensor, for small strains, the matrix of
the Green–St. Venant strain tensor is obtained as follows:
1 2 1
˘
E = (V − I) = (B − I) (4.177)
2 2
    
∂x c ∂x c ∂x c ∂y c

1  ∂x i ∂y i   ∂x i ∂x i  10 
    − 
2  ∂y c ∂y c   ∂x c ∂y c  01 
∂x i ∂y i ∂y i ∂y i