Page 815 - The Mechatronics Handbook

0066_Frame_C25 Page 14 Wednesday, January 9, 2002 7:05 PM

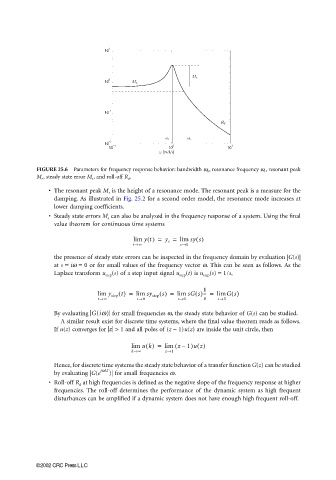
FIGURE 25.6 Parameters for frequency response behavior: bandwidth ω b , resonance frequency ω r , resonant peak
M r , steady state error M e , and roll-off R d .

• The resonant peak M r is the height of a resonance mode. The resonant peak is a measure for the
damping. As illustrated in Fig. 25.2 for a second order model, the resonance mode increases at
lower damping coefficients.
• Steady state errors M e can also be analyzed in the frequency response of a system. Using the final
value theorem for continuous time systems

lim yt() = y s = lim sy s()
t→∞ s→0
the presence of steady state errors can be inspected in the frequency domain by evaluation |G(s)|
at s = iω = 0 or for small values of the frequency vector ω. This can be seen as follows. As the
Laplace transform u step (s) of a step input signal u step (t) is u step (s) = 1/s,

1
lim y step t() = lim sy step s() = lim sG s()-- = lim Gs()
t→∞ s→0 s→0 s s→0

By evaluating G(iw) for small frequencies ω, the steady state behavior of G(s) can be studied.
A similar result exist for discrete time systems, where the final value theorem reads as follows.
z
If u(z) converges for > 1 and all poles of (z − 1)u(z) are inside the unit circle, then
lim uk() = lim ( z 1)uz()
–
k→∞ z→1
Hence, for discrete time systems the steady state behavior of a transfer function G(z) can be studied
iω∆T
by evaluating |G(e )| for small frequencies ω.
• Roll-off R d at high frequencies is defined as the negative slope of the frequency response at higher
frequencies. The roll-off determines the performance of the dynamic system as high frequent
disturbances can be amplified if a dynamic system does not have enough high frequent roll-off.

©2002 CRC Press LLC