Page 820 - The Mechatronics Handbook

066_Frame_C26 Page 5 Wednesday, January 9, 2002 1:58 PM

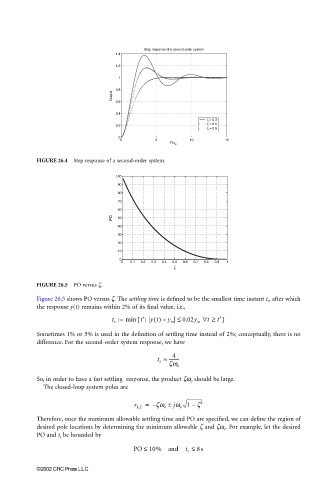
Step response of a second order system
1.4
1.2

1
0.8
Output
0.6
0.4
ζ = 0.3
ζ = 0.5
0.2
ζ = 0.9
0
0 5 10 15
t*ω o
FIGURE 26.4 Step response of a second-order system.

100
90
80
70
60
PO 50
40
30
20
10
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
ζ
FIGURE 26.5 PO versus z.

Figure 26.5 shows PO versus ζ. The settling time is defined to be the smallest time instant t s , after which
the response y(t) remains within 2% of its final value, i.e.,
t s : min t′: yt() y ss ≤ 0.02y ss t ≥ t′}
{
=
∀
–
Sometimes 1% or 5% is used in the definition of settling time instead of 2%; conceptually, there is no
difference. For the second-order system response, we have
4
t s ≈ ---------
zw o
So, in order to have a fast settling response, the product zω o should be large.
The closed-loop system poles are

r 1,2 = – zw o ± jw o 1 z 2
–
Therefore, once the maximum allowable settling time and PO are specified, we can define the region of
desired pole locations by determining the minimum allowable ζ and ζω o . For example, let the desired
PO and t s be bounded by

PO ≤ 10% and t s ≤ 8s

©2002 CRC Press LLC