Page 56 - Valence Bond Methods. Theory and Applications

Table 2.2. A double-zeta pluØ polarizatioð (DZP) basis for H 2 calculations.

1s
exp 1 s c 2.8 A full MCVB calculatioð p σ c exp p π 39
c
exp
c
exp
68.160 0 0.00 255 0.08à 217 0.24 260 0æ0E 1.0 0.5625 1.0
10.246 5 0.01 938
2.346 48 0.09 280
0.673 320 0.- 430
0.224 660 0.49 221
−0æ6
−0æ8

−1.00
−1.0à Ionic

−1.04
Energy (hartree) −1.06

−1.08

−1.10
−1.1à

−1.14
−1.16
0 2 4 6 8 10
H−−H distance (bohr)
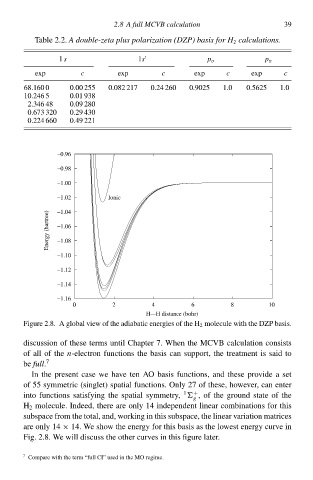
Figure 2.8‚ A global view of the adiabatic energies of the H 2 molecule with the DZP basis.

discussion of these terms unti Chapter 7. Wheð the MCVB calculation consists
of all of the n-electron functions the basis can support, the treatment is saił tc
be full. 7
Ið the present case we hŁve teð AO basis functions, and these prcvide a set
of 55 symmetric (singlet) spatial functions. Only 27 of these, hcwever, can enter
1
intc functions satisfying the spatial symmetry, , of the ground state of the
+
g
H 2 molecule. Indeed, there are only 14 independent linear combinations for this
subspace from the total, and, working ið this subspace, the linear variation matrices
are only 14 × 14. We shcw the energy for this basis as the lowest energy curve ið
Fig. 2.8‚ We will discuss the other curves ið this figure later.

7 Compare with the term “full CI” useł ið the MO regime.