Page 132 - Wind Energy Handbook

106 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

Downwind
" #
1 2 1 2 2 ÷ 2

p þ rU ¼ p 1 þ rU (cos ª 2a) þ sin ª 2a tan
d d 1
2 2 2
where U d is the resultant velocity at the disc.
Subtracting the two equations to obtain the pressure drop across the disc

1 2 ÷ 2 ÷
þ

p p ¼ rU 4a cos ª þ tan sin ª a sec
d d 2 1 2 2
The coefficient of thrust on the disc is therefore,

÷ ÷
C T ¼ 4a cos ª þ tan sin ª a sec 2 (3:111)
2 2

and the power coefficient is

÷ ÷
C P ¼ 4a cos ª þ tan sin ª a sec 2 (cos ª a) (3:112)
2 2

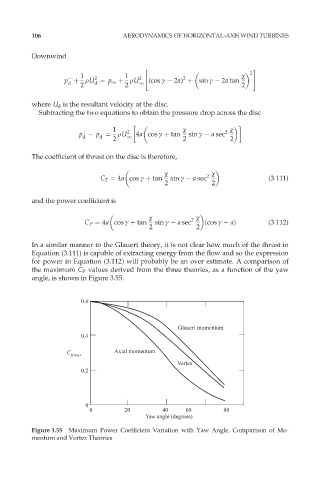
In a similar manner to the Glauert theory, it is not clear how much of the thrust in
Equation (3.111) is capable of extracting energy from the flow and so the expression
for power in Equation (3.112) will probably be an over estimate. A comparison of
the maximum C P values derived from the three theories, as a function of the yaw
angle, is shown in Figure 3.55.

0.6

Glauert momentum
0.4

C Axial momentum
p max
Vortex
0.2

0
0 20 40 60 80
Yaw angle (degrees)
Figure 3.55 Maximum Power Coefficient Variation with Yaw Angle, Comparison of Mo-
mentum and Vortex Theories