Page 179 - Wind Energy Handbook

UNSTEADY FLOW – DYNAMIC INFLOW 153

and n is an integer. Like the Legendre polynomials the Bessel functions are the
solutions to a second-order ordinary differential equation called Bessel’s equation

d 2 d 2 2
2
k y þ k y þ (k n )y ¼ 0
dk 2 dk
Unlike the Legendre polynomials the Bessel functions cannot be expressed in closed
form but only as an infinite series.
Theodorsen’s function is often divided into two functions, one describing the real
part and the other the imaginary part:

C(k) ¼ F(k) þ iG(k) (3:217)

From Jones’ approximation to the Wagner function, Equation (3.214), an approx-
imation to Theodorsen’s function is obtained

0:165 0:335
C(k) ¼ 1 0:0455 0:30 ¼ F(k) ¼ iG(k) (3:218)
1 i 1 i
k k

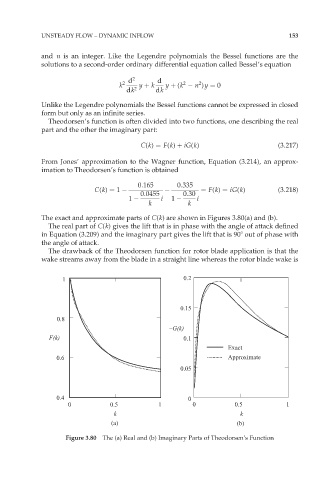
The exact and approximate parts of C(k) are shown in Figures 3.80(a) and (b).
The real part of C(k) gives the lift that is in phase with the angle of attack defined
in Equation (3.209) and the imaginary part gives the lift that is 908 out of phase with
the angle of attack.
The drawback of the Theodorsen function for rotor blade application is that the
wake streams away from the blade in a straight line whereas the rotor blade wake is

1 0.2

0.15
0.8
–G(k)
F(k) 0.1
Exact
0.6 Approximate
0.05

0.4 0
0 0.5 1 0 0.5 1
k k
(a) (b)
Figure 3.80 The (a) Real and (b) Imaginary Parts of Theodorsen’s Function