Page 273 - Wind Energy Handbook

BLADE LOADS DURING OPERATION 247

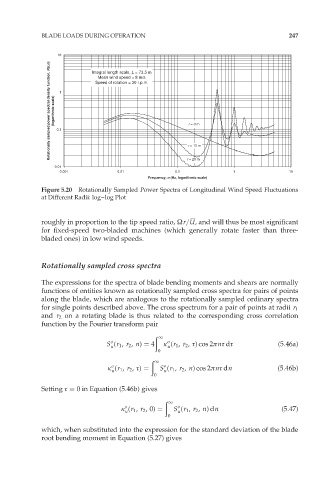
10 Integral length scale, L = 73.5 m
Rotationally sampled power spectral density function, R(r,n) (logarithmic scale) 0.1 1 r = 0 m

Mean wind speed = 8 m/s
Speed of rotation = 30 r.p.m.

r = 10 m

0.01 r = 20 m
0.001 0.01 0.1 1 10
Frequency, n (Hz, logarithmic scale)
Figure 5.20 Rotationally Sampled Power Spectra of Longitudinal Wind Speed Fluctuations
at Different Radii: log–log Plot

roughly in proportion to the tip speed ratio, Ùr=U, and will thus be most significant
for fixed-speed two-bladed machines (which generally rotate faster than three-
bladed ones) in low wind speeds.

Rotationally sampled cross spectra

The expressions for the spectra of blade bending moments and shears are normally
functions of entities known as rotationally sampled cross spectra for pairs of points
along the blade, which are analogous to the rotationally sampled ordinary spectra
for single points described above. The cross spectrum for a pair of points at radii r 1
and r 2 on a rotating blade is thus related to the corresponding cross correlation
function by the Fourier transform pair
ð
1
o
o
S (r 1 , r 2 , n) ¼ 4 k (r 1 , r 2 , ô) cos 2ðnô dô (5:46a)
u u
0
ð
1
o
o
k (r 1 , r 2 , ô) ¼ S (r 1 , r 2 , n)cos 2ðnô dn (5:46b)
u
u
0
Setting ô ¼ 0 in Equation (5.46b) gives
ð 1
o
o
k (r 1 , r 2 ,0) ¼ S (r 1 , r 2 , n)dn (5:47)
u
u
0
which, when substituted into the expression for the standard deviation of the blade
root bending moment in Equation (5.27) gives