Page 101 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P2: —/—
QC: —/—
T1: IML
P1: KVU/—
AT029-Manual-v7.cls
AT029-02
August 16, 2007
AT029-Manual
16:6
2. CHARACTERIZATION AND PROPERTIES OF PURE HYDROCARBONS 81
they obtained the coefficients for T c , P c , and V c in Eq. (2.38)
with use of d 20 (liquid density at 20 C and 1 atm in g/cm )
3
◦
b c
instead of SG (T c , P c , V c = aT d ). They reported the coeffi-
20
b
cients as [87] T c /K (a = 18.2394, b = 0.595251, c = 0.347420),
P c /bar (a = 2.95152 × 10 , b =−2.2082, c = 2.22086), and
7
−5
3
V c /cm /mol (a = 8.22382 × 10 , b = 2.51217, c =−1.62214).
Equation (2.38) with these coefficients have not been exten-
sively tested against data on properties of petroleum fractions
as yet but for more than 300 pure hydrocarbons gives average Acentric Factor
errors of 0.7, 3.8, and 2.9% for T c , P c , and V c , respectively [87].
2.9.4 Evaluation of Methods of Estimation
of Acentric Factor and Other Properties
For the calculation of the acentric factor of pure hydrocar-
bons Eq. (2.42) is quite accurate and will be used in Chapter 3
for the pseudocomponent method. Firoozabadi suggests that
for aromatics with M > 800, ω = 2. Generally there are three
methods for the estimation of the acentric factor of undefined
petroleum fractions. Perhaps the most accurate method is to
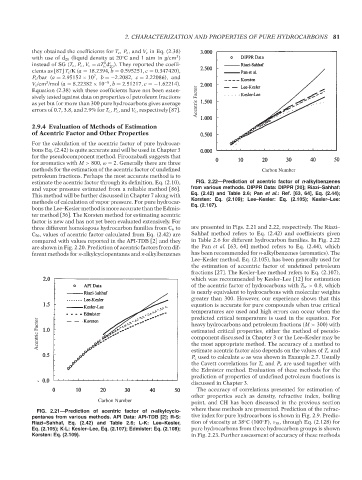
estimate the acentric factor through its definition, Eq. (2.10), FIG. 2.22—Prediction of acentric factor of n-alkylbenzenes
and vapor pressure estimated from a reliable method [86]. from various methods. DIPPR Data: DIPPR [20]; Riazi–Sahhaf:
This method will be further discussed in Chapter 7 along with Eq. (2.42) and Table 2.6; Pan et al.: Ref. [63, 64], Eq. (2.44);
methods of calculation of vapor pressure. For pure hydrocar- Korsten: Eq. (2.109); Lee–Kesler: Eq. (2.105); Kesler–Lee:
bons the Lee–Kesler method is more accurate than the Edmis- Eq. (2.107).
ter method [36]. The Korsten method for estimating acentric
factor is new and has not yet been evaluated extensively. For
three different homologous hydrocarbon families from C 6 to are presented in Figs. 2.21 and 2.22, respectively. The Riazi–
C 50 , values of acentric factor calculated from Eq. (2.42) are Sahhaf method refers to Eq. (2.42) and coefficients given
compared with values reported in the API-TDB [2] and they in Table 2.6 for different hydrocarbon families. In Fig. 2.22
are shown in Fig. 2.20. Prediction of acentric factors from dif- the Pan et al. [63, 64] method refers to Eq. (2.44), which
ferent methods for n-alkylcyclopentanes and n-alkylbenzenes has been recommended for n-alkylbenzenes (aromatics). The
Lee–Kesler method, Eq. (2.105), has been generally used for
the estimation of accentric factor of undefined petroleum
fractions [27]. The Kesler–Lee method refers to Eq. (2.107),
which was recommended by Kesler–Lee [12] for estimation
of the acentric factor of hydrocarbons with T br > 0.8, which
is nearly equivalent to hydrocarbons with molecular weights
greater than 300. However, our experience shows that this
equation is accurate for pure compounds when true critical
temperatures are used and high errors can occur when the
predicted critical temperature is used in the equation. For
Acentric Factor estimated critical properties, either the method of pseudo-
heavy hydrocarbons and petroleum fractions (M > 300) with
component discussed in Chapter 3 or the Lee–Kesler may be
the most appropriate method. The accuracy of a method to
estimate acentric factor also depends on the values of T c and
P c used to calculate ω as was shown in Example 2.7. Usually
the Cavett correlations for T c and P c are used together with
the Edmister method. Evaluation of these methods for the
prediction of properties of undefined petroleum fractions is
discussed in Chapter 3.
The accuracy of correlations presented for estimation of
other properties such as density, refractive index, boiling
Carbon Number point, and CH has been discussed in the previous section
where these methods are presented. Prediction of the refrac-
FIG. 2.21—Prediction of acentric factor of n-alkylcyclo-
pentanes from various methods. API Data: API-TDB [2]; R-S: tive index for pure hydrocarbons is shown in Fig. 2.9. Predic-
◦
◦
Riazi–Sahhaf, Eq. (2.42) and Table 2.6; L-K: Lee–Kesler, tion of viscosity at 38 C (100 F), ν 38 , through Eq. (2.128) for
Eq. (2.105); K-L: Kesler–Lee, Eq. (2.107); Edmister: Eq. (2.108); pure hydrocarbons from three hydrocarbon groups is shown
Korsten: Eq. (2.109). in Fig. 2.23. Further assessment of accuracy of these methods

--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT