Page 344 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P2: IML/FFX
T1: IML
P1: IML/FFX
QC: IML/FFX
June 22, 2007
AT029-Manual-v7.cls
AT029-07
17:40
AT029-Manual
324 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
TABLE 7.11—Experimental data on heat of vaporization of some coal liquid fractions with calculated
basic parameters [28].
vap
Fraction (a) T b ,K SG H nbp , kJ/kg M T c ,K P c ,bar ω
5HC 433.2 0.8827 309.4 121.8 649.1 33.1 0.302
8HC 519.8 0.9718 281.4 162.7 748.1 27.1 0.394
11HC 612.6 1.0359 269.6 223.1 843.1 21.5 0.512
16HC 658.7 1.0910 245.4 247.9 896.4 20.5 0.552
17HC 692.6 1.1204 239.3 272.0 932.2 19.4 0.590
M from Eq. (2.51), T c and P c from Eqs. (2.63) and (2.64), ω from Eq. (2.108). Experimental value on T b , SG, and H nbp
are taken from J. A. Gray, Report DOE/ET/10104-7, April 1981; Department of Energy, Washington, DC and are also
given in Ref. [28].
TABLE 7.12—Evaluation of various methods of prediction of heat of vaporization of petroleum
fractions with data of Table 7.11.
Riedel, Eq. (7.54) Chen, Eq. (7.55) RD, Eq. (7.56) MLK, Eq. (7.58)
vap
Fraction H bp exp. Calc. %Dev. Calc. %Dev. Calc. %Dev. Calc. %Dev.
5HC 309.4 305.9 −1.1 303.9 −1.8 311.8 0.8 304.7 −1.5
8HC 281.4 282.5 0.4 278.9 −0.9 287.7 2.2 276.6 −1.7
11HC 269.6 252.2 −6.4 246.3 −8.6 253.2 −6.1 240.5 −10.8
16HC 245.4 248.5 1.3 241.5 −1.6 247.6 0.9 234.7 −4.4
17HC 239.3 241.8 1.0 233.8 −2.3 239.0 −0.1 226.2 −5.5
%AAD . . . . . . 2.0 . . . 3.0 . . . 2.0 . . . 4.8
Values of M, T c , P c ,and ω from Table 7.10 have been used for the calculations. RD refers to Riazi–Daubert method or
Eq. (7.56) in terms of T b and SG as given in Table 7.10. MLK refers to modified Lee–Kesler correlation or Eq. (7.58).
vap
In use of Eq. (7.58), values of H nbp have been obtained by correcting estimated values at T r = 0.8to T r = T rb , using
Eq. (7.57).
vap
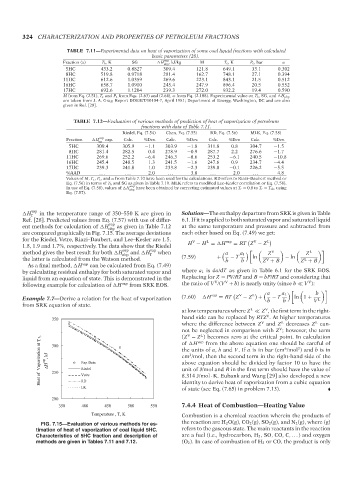
H in the temperature range of 350–550 K are given in Solution—The enthalpy departure from SRK is given in Table
T
Ref. [28]. Predicted values from Eq. (7.57) with use of differ- 6.1. If it is applied to both saturated vapor and saturated liquid
vap
ent methods for calculation of H nbp as given in Table 7.12 at the same temperature and pressure and subtracted from
are compared graphically in Fig. 7.15. The average deviations each other based on Eq. (7.49) we get:
for the Riedel, Vetre, Riazi–Daubert, and Lee–Kesler are 1.5, V L vap V L
1.8, 1.9 and 1.7%, respectively. The data show that the Riedel H − H = H = RT Z − Z
vap
method gives the best result for both H nbp and H T vap when a a 1 Z V Z L
the latter is calculated from the Watson method. (7.59) + b − T b ln Z + B − ln Z + B
L
V
As a final method, H vap can be calculated from Eq. (7.49)
by calculating residual enthalpy for both saturated vapor and where a 1 is da/dT as given in Table 6.1 for the SRK EOS.
liquid from an equation of state. This is demonstrated in the Replacing for Z = PV/RT and B = bP/RT and considering that
V
V
V
following example for calculation of H vap from SRK EOS. the ratio of V /(V + b) is nearly unity (since b V ):
a a 1 b
vap
L
V

Example 7.7—Derive a relation for the heat of vaporization (7.60) H = RT Z − Z + b − T b ln 1 + V L
from SRK equation of state.
L
V
at low temperatures where Z Z , the first term in the right-
V
hand side can be replaced by RTZ . At higher temperatures
350
L
L
V
where the difference between Z and Z decreases Z can-
V
not be neglected in comparison with Z ; however, the term
V
L
Heat of Vaporization at Τ b, ΔH vap , kJ 300 Exp. Data the units of a, b and V.If a is in bar (cm /mol ) and b is in
(Z − Z ) becomes zero at the critical point. In calculation
vap
from the above equation one should be careful of
of H
2
6
cm /mol, then the second term in the right-hand side of the
3
above equation should be divided by factor 10 to have the
unit of J/mol and R in the first term should have the value of
Riedel
250
Vetre
RD
identity to derive heat of vaporization from a cubic equation
LK 8.314 J/mol · K. Eubank and Wang [29] also developed a new
of state (see Eq. (7.65) in problem 7.13).
200
350 400 450 500 550 7.4.4 Heat of Combustion—Heating Value
Temperature , T, K Combustion is a chemical reaction wherein the products of
the reaction are H 2 O(g), CO 2 (g), SO 2 (g), and N 2 (g), where (g)
FIG. 7.15—Evaluation of various methods for es-
timation of heat of vaporization of coal liquid 5HC. refers to the gaseous state. The main reactants in the reaction
Characteristics of 5HC fraction and description of are a fuel (i.e., hydrocarbon, H 2 , SO, CO, C, . . . ) and oxygen
methods are given in Tables 7.11 and 7.12. (O 2 ). In case of combustion of H 2 or CO, the product is only
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT